三角関数入門
唐突に見せられたこの文字列を見て拒絶反応を起こしてる人いませんか？
三角関数よりも他の学問を学ぶべきみたいなことを仰る方が実際にいるくらいですので、特に小中学生にはとてつもなくハードルが高い数学用語に聞こえているかもしれません。
勿論奥深くまで学ぼうとすると難しいのですが、表面に触れる程度であれば実はそこまで難しくなかったりします。
足し算・引き算・三角比という言葉がある#1ように、あらゆる学問の基礎・土台である三角比・三角関数についてこの記事で軽く学んでいきましょう。
概要 - Abstract
この記事では三角比とは何か？という初歩の初歩から三角関数の導入までを軽く扱います。また関数とは何か？などの三角関数を理解するために必要な知識も扱います。
記事の途中で理解度を確認するための練習問題もいくつか提示しました。三角比・三角関数が初めての人は練習問題（特に発展問題）すらもとても難しく感じるかもしれません。しかし一旦答えを見て理解してからもう一度解き直すということを何度も繰り返せば気づけば簡単に感じられるようになるはずです。
ではぜひ手元に紙とペンを用意して数学をお楽しみください。
対象読者
- ロボット製作にあたって数学につまづいている小中学生
- 高校卒業以降、三角関数を退け続けた人生を送っている方
- ちょっと知的な読み物を欲している方
（学生や動物園生#2の方、理系のお仕事されている方には簡単すぎて物足りない記事になっていると思います。）
必要知識
小学校卒業程度の算数力に加えて正負の数の計算ができればOKです。中学校卒業以上の数学力があればより面白いかもしれません。
Note
本編に入る前にこの記事で説明しないこと、省いて説明することをあらかじめ明示します。この項は読み飛ばしてもらって構いません。
- 弧度法には触れません。全て60分法で説明します。
- もちろん正弦定理、余弦定理、加法定理等の説明もしません。
相似と比
ではここで三角定規を取り出してみましょう。正三角形の半分の形のやつです。
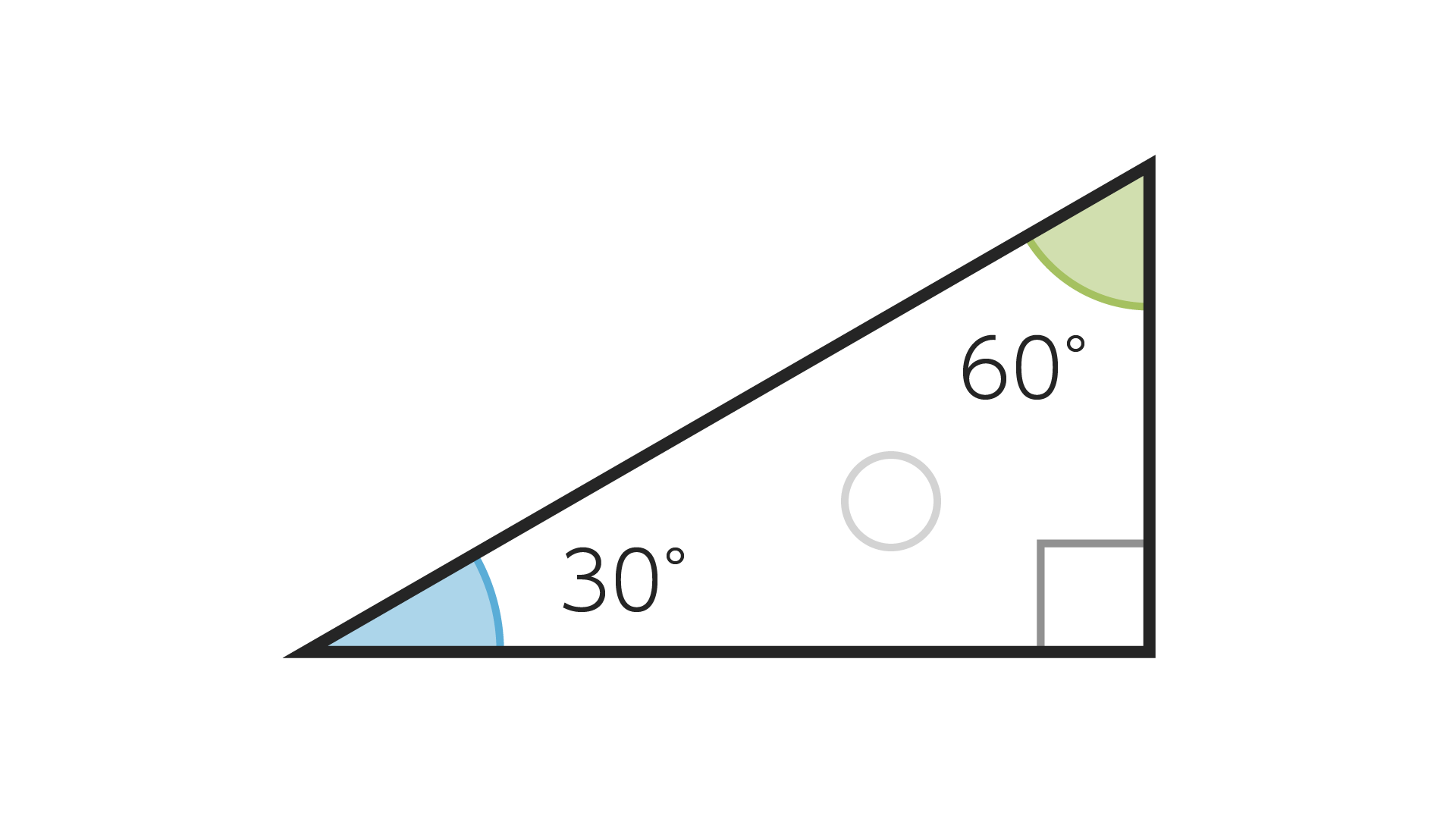
この時のそれぞれの角の大きさは30°, 60°, 90°ですね。
この三角形の斜辺（=斜めの辺）の長さを2とした時、対辺（=縦の辺）の長さは1、底辺（=横の辺）の長さは$\sqrt{3}(\fallingdotseq1.7320508…)$になることが知られています。
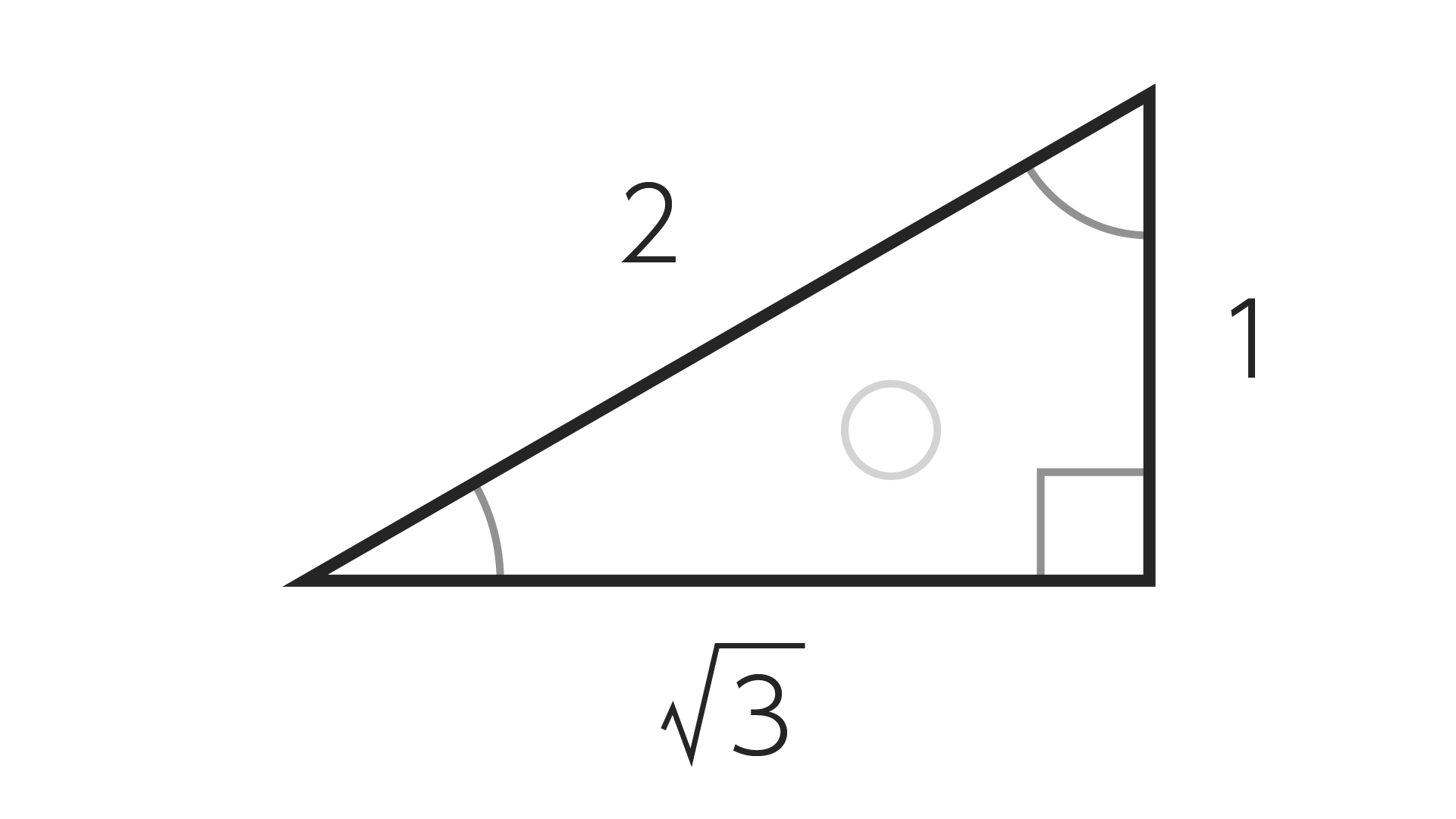
これと同じ三角定規を友達に借りて2つ並べてみると正三角形になりますね。正三角形は全ての辺の長さが等しいです。つまり対辺はその正三角形の一辺の半分なので長さが1になります。
底辺が$\sqrt{3}$になる理由は神のみぞ知る領域#3なので今回は飛ばします。
👀補足説明：$\sqrt{3}$ってなに？
例えば3を2回かけると3×3=9になりますね。この逆の計算を考えてみましょう。
$a\times a=9$とするとき$a$の値は何になるでしょうか。$a=±3$ですね。（正の数だけでなく、負の数同士の積も正になることに注意）
では$b\times b=3$とするとき$b$の値は何になるでしょうか。これは計算していくと$b=±1.7320508…$と無限に続いていきます。どこかで割り切れるというようなことはありません。
この例のように2回かけたら$x$になる数字を表す記号として$\sqrt{x}$（読み：ルート）が用意されています。例えば先の例の±1.7320508…という数字は$±\sqrt{3}$と表すことができます。
例: $\sqrt{9}=3,\sqrt{3}=1.7320508…$
（この説明がよくわからなかった人は記事中の$\sqrt{3}$を全て1.7320508…に置き換えて読んでも大丈夫です。）
ここで比という概念を持ち出してみましょう。この三角定規の斜辺：対辺：底辺の比は
\[2:1:\sqrt{3}\]になります。以降これを辺の比と言うことにします。
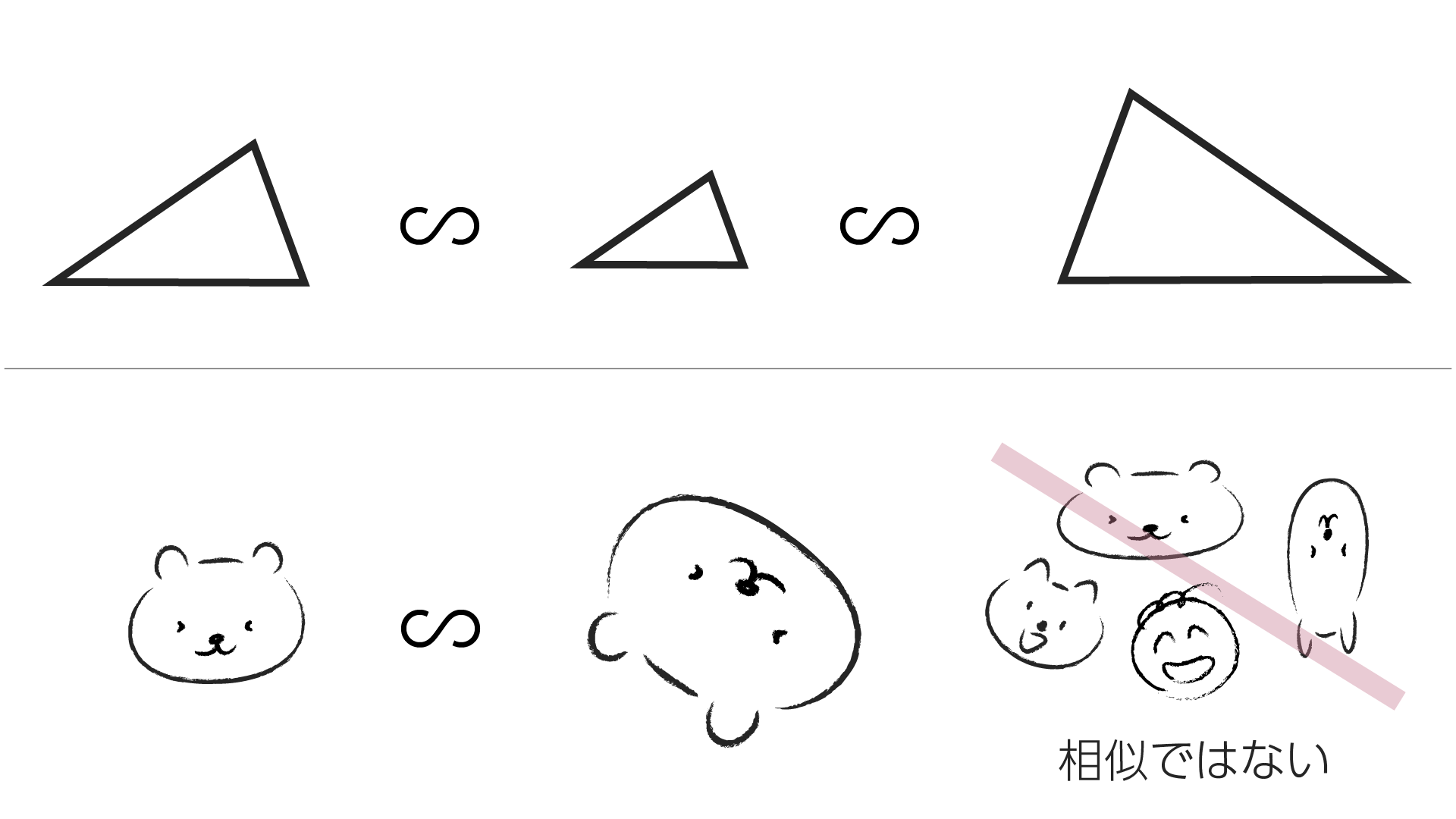
この例のように「大きさは違うけど形は同じ」ということを数学の言葉で相似といい、S字フックのような記号で表します。
- 形が同じものは大きさが違っても裏返ってても向きが異なっても相似である
- 縦横に引き伸ばされたようなものは形が違うので相似ではない
- そもそも違う形状ももちろん相似ではない
相似の図形同士には以下が成り立ちます
- 辺の比は変わらない
- 対応する角の大きさは変わらない
逆にこのことから対応する角の大きさが等しい図形同士は相似であると言えます。
したがって、対応する角の大きさが全て等しければ辺の比も等しくなります。 ←超重要①
🤔この説明がちょっと難しかった人へ
小学校6年生の算数の教科書の「図形の拡大と縮小」のページを読み直してみよう。
この相似の概念を頭に入れた状態で次の図を見てください。この部分がこの記事の要であり一番重要なところです。
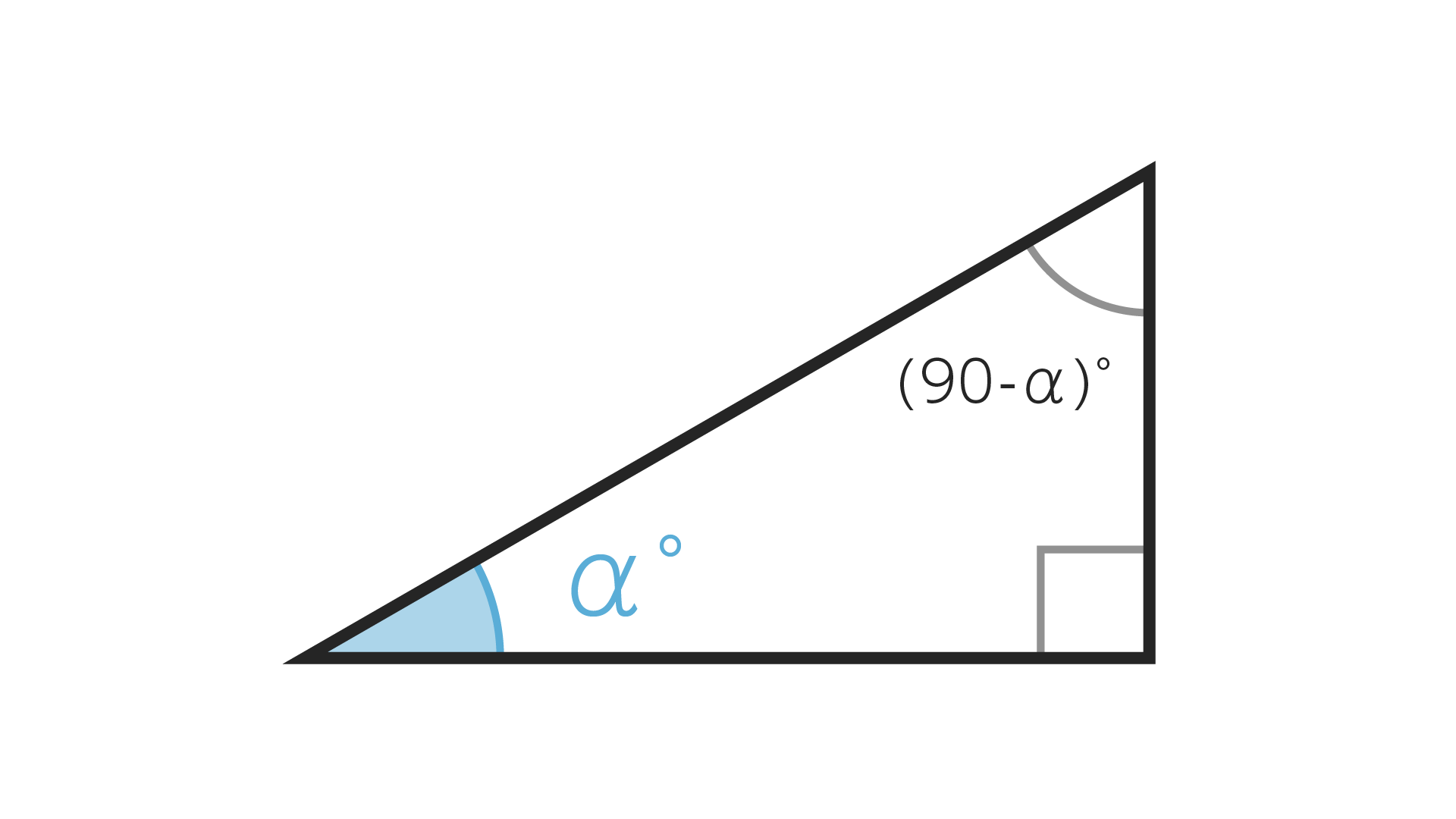
三角形の内角の和は180°です。直角三角形の3つの角のうち1つは90°、もう一つを$\alpha^\circ$（アルファ）としたとき残りの一つの角は
\[\begin{split}180^\circ-90^\circ-\alpha^\circ=(90-\alpha)^\circ\end{split}\]となります。つまり直角三角形の場合は
2つある直角でない角のうち1つでも定まればもう一つも定まり、全ての角の大きさが定まります。 ←超重要②
超重要①と②から「$\alpha^\circ$が等しい三角形同士の辺の比は等しい」と言えます。つまり$\alpha^\circ$さえ与えられれば辺の比を求められます！
この章のPoint
- 相似の図形は対応する角の大きさが等しく、辺の比は変わらない
- 直角三角形では直角でない1つの角が同じ直角三角形同士は相似になる
三角比
とある偉い人が「$\alpha^\circ$が等しい直角三角形同士は必ず相似であり、辺の比も等しい」ということは「$\alpha^\circ$をもとに三角形の辺の比を表せるのでは…？」と考えました。
これが本日のお題、三角比です。
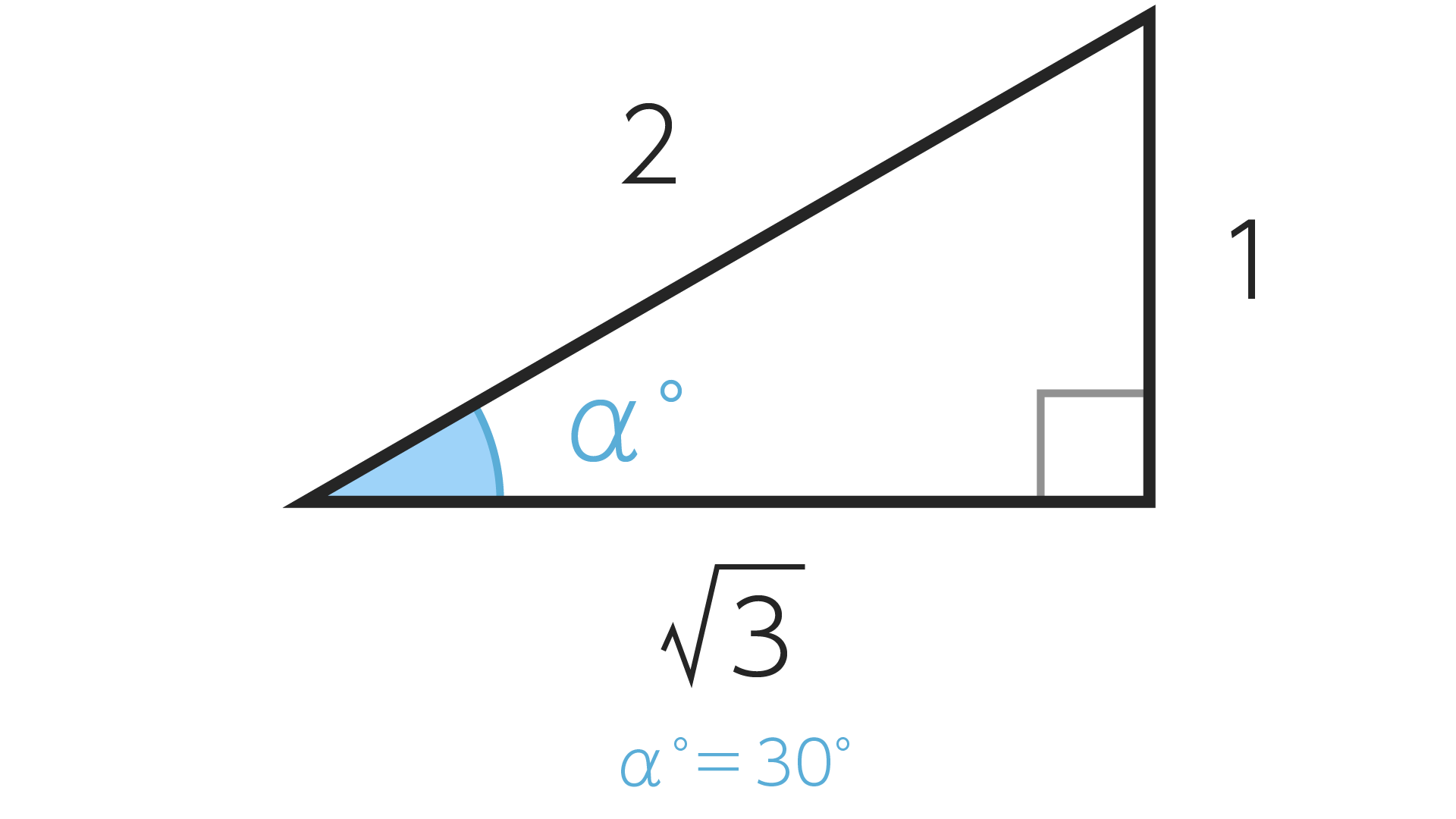
この図を使って$\alpha^\circ$の三角比を実際に求めながらsin, cos, tanと学んでいきましょう。
sin
斜辺の長さに対する対辺の長さはsinを使って表します。
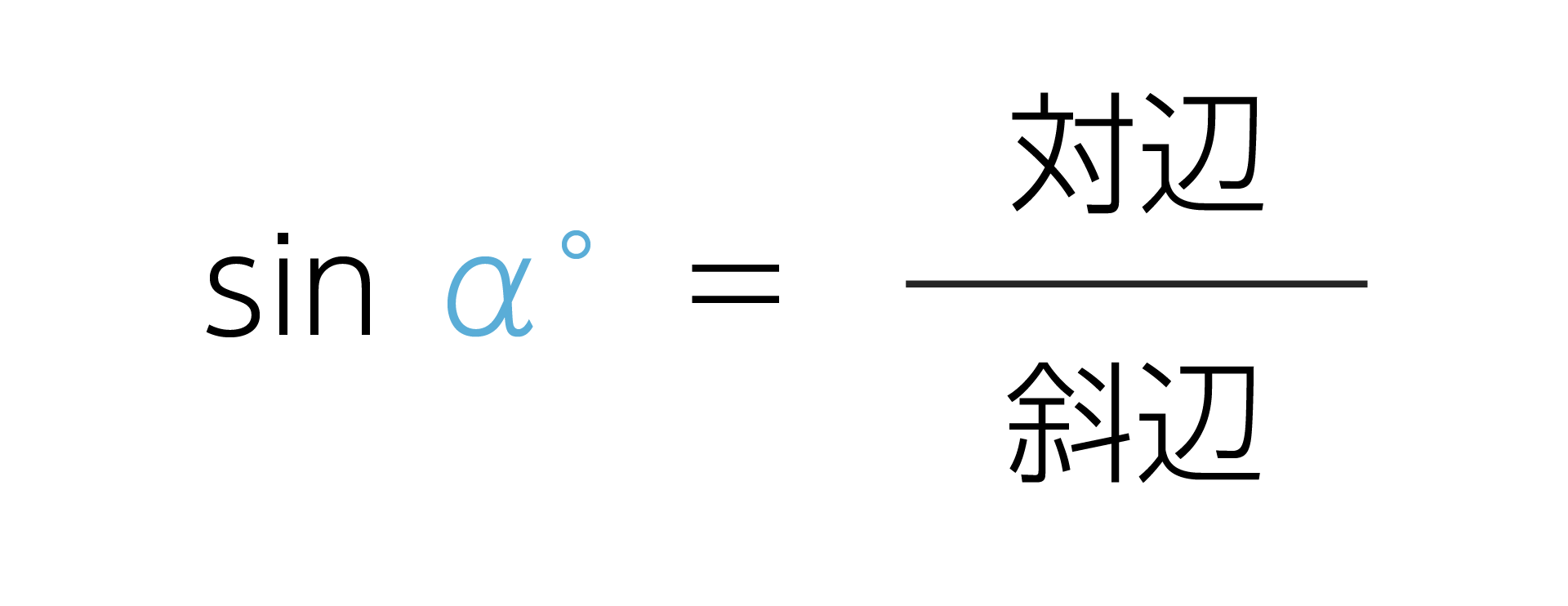
この例だと、$\alpha^\circ=30^\circ$で斜辺は2、対辺は1なので
\[\begin{split}\sin{\alpha^\circ} &= \sin{30^\circ}\\ &=\frac{1}{2}\end{split}\]となります。言いかえると、sinとは斜辺の長さを何倍すれば対辺の長さになるかなので、もちろん斜辺の長さに$\sin{\alpha^\circ}$をかけると対辺の長さになります。
\[\begin{split}斜辺\times\sin\alpha^\circ&=2\times\sin{30^\circ} \\&= 2\times\frac{1}{2}\\ &=1\end{split}\]cos
斜辺の長さに対する底辺の長さはcosを使って表します。
この例だと、$\alpha^\circ=30^\circ$で斜辺は2、底辺は$\sqrt{3}$なので
\[\begin{split}\cos{\alpha^\circ} &= \cos{30^\circ}\\ &=\frac{\sqrt{3}}{2}\end{split}\]となります。sinと同様にcosとは斜辺の長さを何倍すれば底辺の長さになるかなので、斜辺の長さに$\cos{\alpha^\circ}$をかけると底辺の長さになります。
\[\begin{split}斜辺\times\cos\alpha^\circ&=2\times\cos{30^\circ} \\&= 2\times\frac{\sqrt{3}}{2}\\ &=\sqrt{3}\end{split}\]tan
底辺の長さに対する対辺の長さはtanを使って表します。
この例だと、$\alpha^\circ=30^\circ$で底辺は$\sqrt{3}$、対辺は1なので
\[\begin{split}\tan{\alpha^\circ} &= \tan{30^\circ}\\ &=\frac{1}{\sqrt{3}}\end{split}\]となります。sin, cosと同様にtanとは底辺の長さを何倍すれば対辺の長さになるかなので、底辺の長さに$\tan{\alpha^\circ}$をかけると対辺の長さになります。
\[\begin{split}底辺\times\tan\alpha^\circ&=2\times\tan{30^\circ} \\&= \sqrt{3}\times\frac{1}{\sqrt{3}}\\ &=1\end{split}\]これで一通り30°の三角比を求めることができました。まとめてみましょう。
\[\begin{split}\sin30^\circ &= \frac{1}{2} \\ \cos30^\circ &= \frac{\sqrt{3}}{2} \\ \tan30^\circ &= \frac{1}{\sqrt{3}}\end{split}\]基本問題
下の図を用いて$\sin\alpha^\circ, \cos\alpha^\circ ,\tan\alpha^\circ$の値をそれぞれ求めよ。
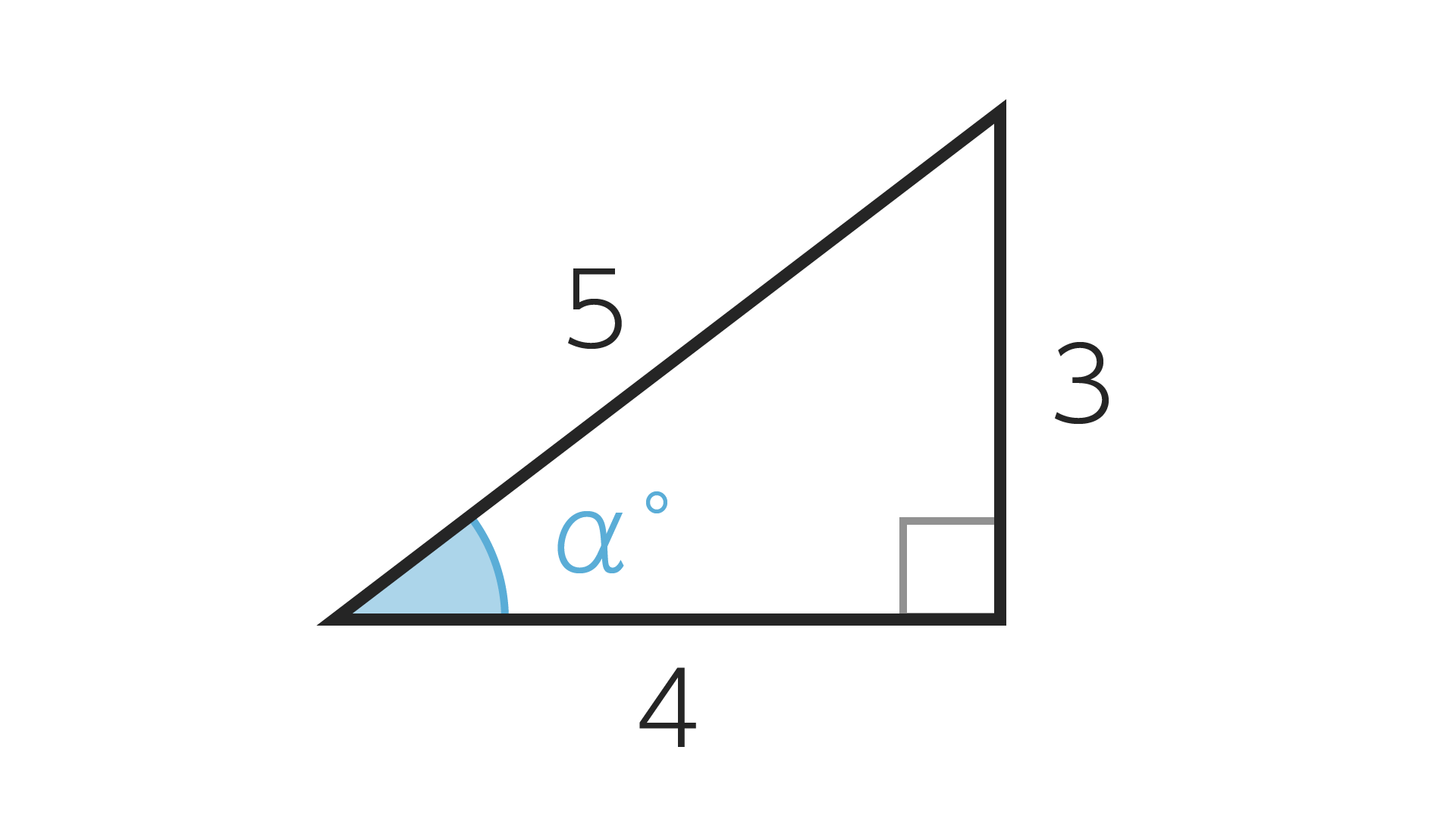
答え（ぼかしをタップするとみれます）
$\sin\alpha=\frac{3}{5},\cos\alpha=\frac{4}{5}, \tan\alpha=\frac{3}{4}$
発展問題
練習問題 #1の図を用いて$\sin(90^\circ-\alpha)$の値を求めよ。
答え（ぼかしをタップするとみれます）
$\sin\alpha=\frac{4}{5}$
解説を詳しく見る 見なかったことにする
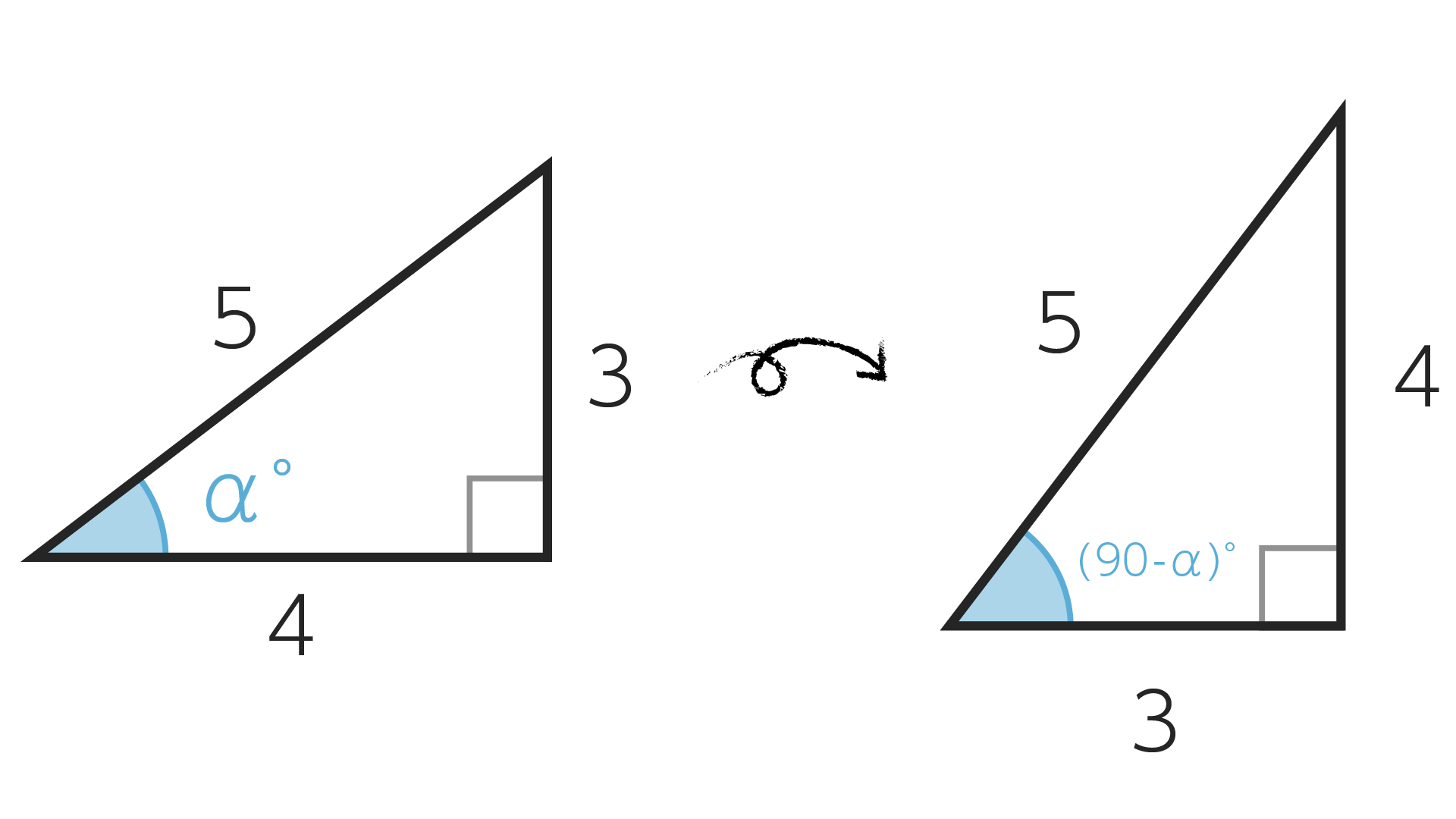このように向きをひっくり返して考えてみましょう。
関数とは？
関数とはパズルのことです！！！（？？？）
唐突ですが「3を足す$(x)=x+3$」という関数があったとします。これをイメージしやすくするとこんな感じです。
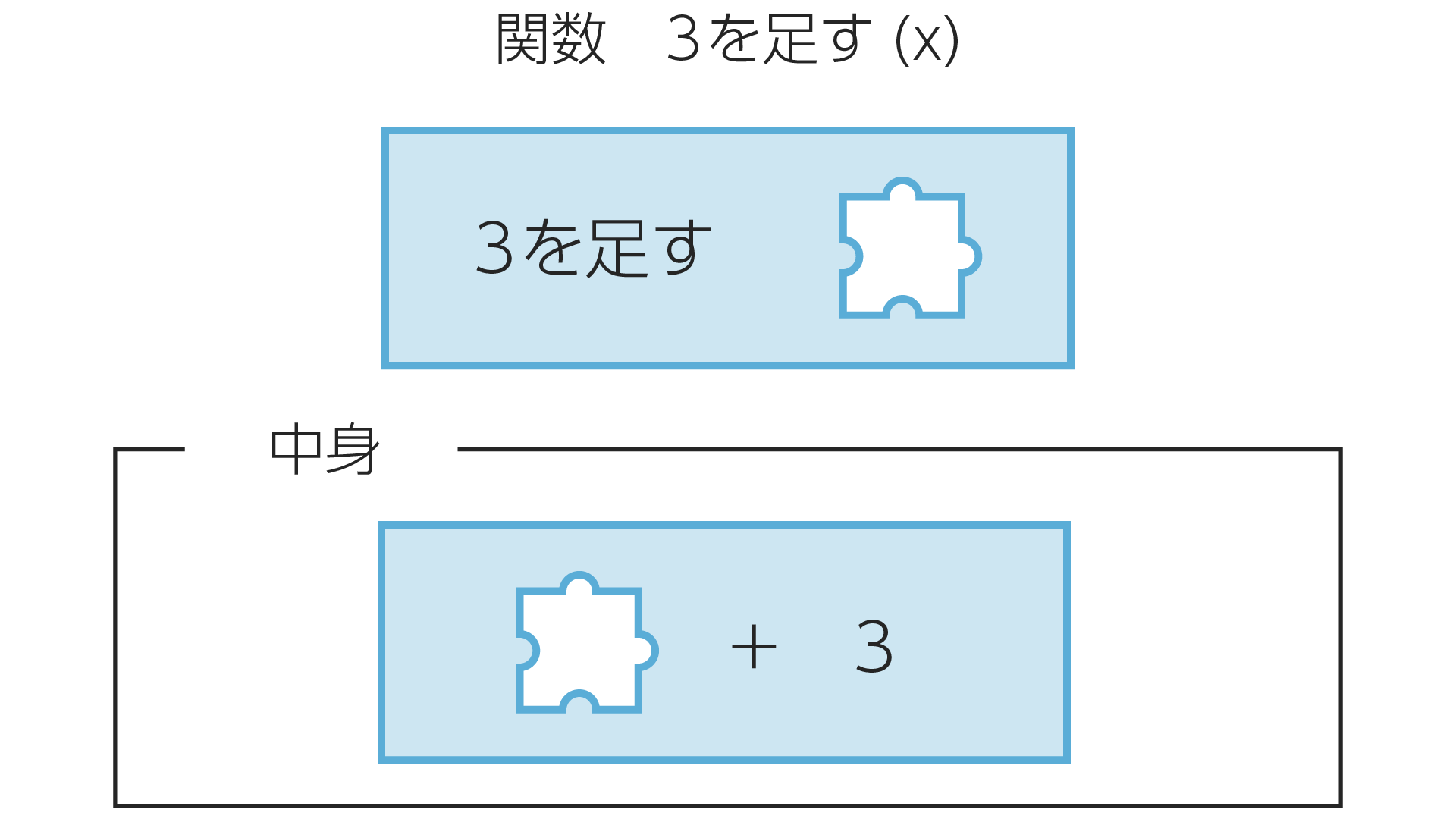
「3を足す」は関数の名前です。今回はわかりやすさのために日本語で書いてますが、普通はアルファベットを使います。（例: $f(x), g(x)$ ）
$x$は「ここにピースをはめてね」という意味を表しています。「3を足す$x$」と書いてしまうとどこまでが関数の名前かわからなくなるのでそれを防ぐために括弧をつけます。
では試しに「8」のピースを当てはめて「3を足す$(8)$」の値を計算してみましょう。
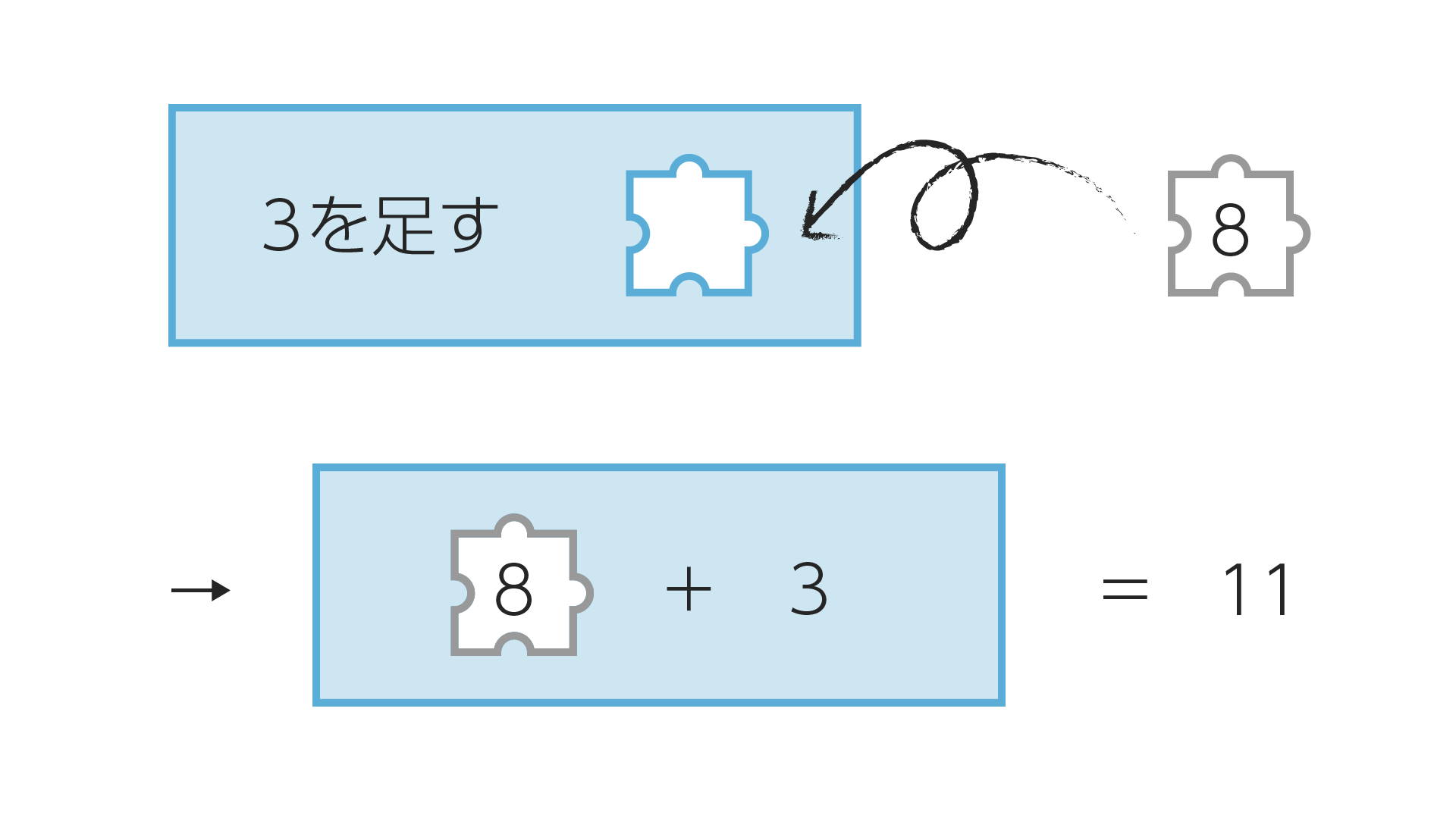
関数のイメージは掴めましたか？関数を使うと入力（パズルのピース）と完成した式との関係を示すことができます。
このような式で$x$と$y$の関係を表せるとき、$y$は$x$の関数であると言います。「$x$が与えられたとき$y$がただ一つに定まる」ということです。
\[y=f(x)\]難しい感じがしますが実は小学5年生「ともなって変わる量」の算数の単元でやっています。そうですね、おなじみ比例・反比例も関数として考えることができます。 たとえば、
\[□ =5\times○\]という式があったとき$□$を$y$、$○$を$x$と考えると
\[y=5x\]と表せます。$f(x)=5x$とすると…
\[y=f(x)\]の形になりましたね。立派な関数であることがわかります。
🍰小学生向け補足説明
算数の一歩先の数学の世界では掛け算をとてもよく使うので、文字と文字、または文字と数の計算であれば掛け算の記号「×」を省いて記すことができます。
これはOK🙆: $5x = 5\times x, xy = x\times y$
これはダメ🙅: $53 = 5\times3$
基本問題
二つの関数$f(x)=5x+2,g(x)=\frac{10}{x}$があるとき、次の値を求めよ。
$(1) f(5)$
$(2) g(3)$
$(3) f(2)\times g(5)$
$(4) \frac{g(2)}{f(4)}$
答え（ぼかしをタップするとみれます）
$(1) 27$
$(2) \frac{10}{3}$
$(3) 24$
$(4) \frac{5}{22}$
解説
(1),(2)はそのまま$x$に当てはめるだけでOKです。(3),(4)はそれぞれの関数の値を求めてから計算してみましょう。
途中式を詳しく見る 見なかったことにする
(1) $$\begin{split}f(5)&=5\times5+2\\ &=27\end{split}$$ (2) $$\begin{split} g(3)&=\frac{10}{3}\\ &= \frac{10}{3} \end{split}$$ (3) $$\begin{split} f(2)&=5\times2+2\\ &=12\\ \\ g(5)&=\frac{10}{5}\\ &=2\\ \\ f(2)\times g(5)&=12\times2\\ &=24 \end{split}$$ (4) $$\begin{split} f(4)&=5\times4+2\\ &=22\\ \\ g(2)&=\frac{10}{2}\\ &=5\\ \\ \frac{g(2)}{f(4)}&=\frac{5}{22} \end{split} $$三角関数
数字を与えれば何か一つの数字がもとまる…なんかモヤモヤしませんか？
さっきやりましたよね？覚えてますよね…？
そうです、三角比ですね。（強引）
しかし、ある致命的な欠点があります。90°以上の角が与えられた時に成立しないということです。
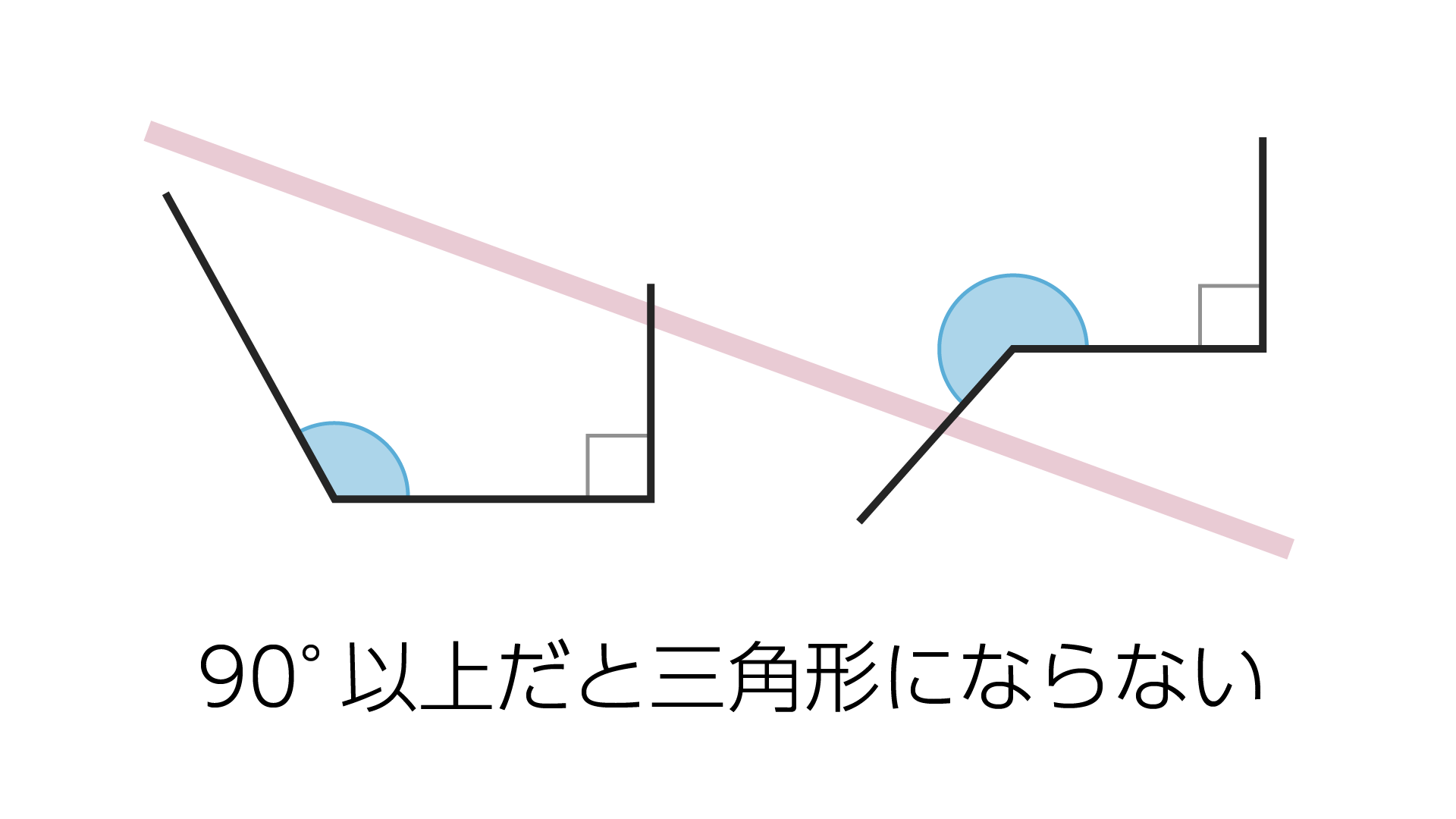
三角比の場合は90°までの角に対する値を定義していましたが、90°以上のすべての角に対して成立するように考え方を拡張してみます。ここからは三角関数の話です。
平面上に半径rの円を書き、こんな感じで角$\theta$（シータ）を書きます。
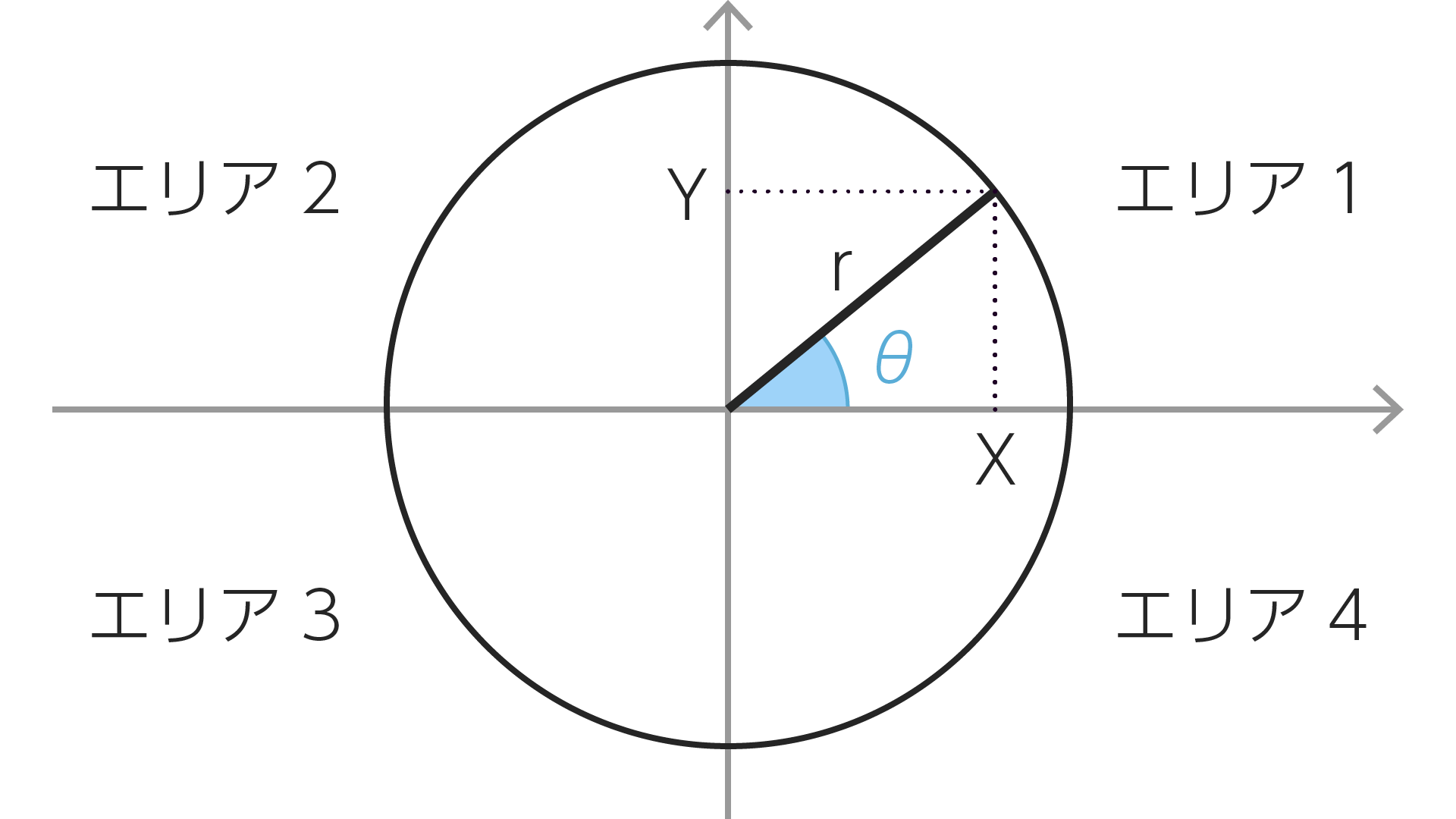
四分割した時の右上をエリア1として反時計回りにエリア2、3、4と呼ぶことにします。#5
😡発展：$\alpha$とか$\theta$とかギリシャ文字やめろや！！
確かにギリシャ文字に慣れてない人は難しいかもしれないですが理由があります。トイレとかが詰まった時に使うやつのことをほとんどの人が「スッポン」というでしょうが、正式な名前は「ラバーカップ」と言います。でも名前が長いので言いにくいですよね。そこでみんながある程度共通して「スッポン」という略称を使います。
このような感じで角を表す時には数学の世界では$\theta$をよく使います。他の記事や本を読んでる時に$\theta$が出てきたら多くの場合角のことを指しているはずです。式に使われる記号がその式の意味を教えてくれるわけです。
$\alpha$に関しては何にでも使われがちな便利屋さんです。$x,y,z$くらいの軽いノリで使われます。誰でもいいから僕と結婚しよう！！って言ってる人とやってることは変わりません。
この記事では三角比の話をしているときは$\alpha$、三角関数の話をしているときは$\theta$を使うことで混同を防ぎました。
この時のXは三角比でいう底辺に相当します。Yは対辺に相当します。円の半径rは斜辺に相当します。
🦊この説明がちょっと難しかった人へ
小学4年生算数「ものの位置の表し方」のページを読み直してみよう。
このように考えると次のようにsin,cos,tanを定義できます。
\[\begin{split} \sin\theta&=\frac{Y}{r}\\ \\ \cos\theta&=\frac{X}{r}\\ \\ \tan\theta&=\frac{Y}{X} \end{split}\]三角比との大きな違いはX・Yの取りうる値が負の数になることがあるということです。具体的にはXはエリア2・3では負の数に、Yはエリア3・4では負の数になります。
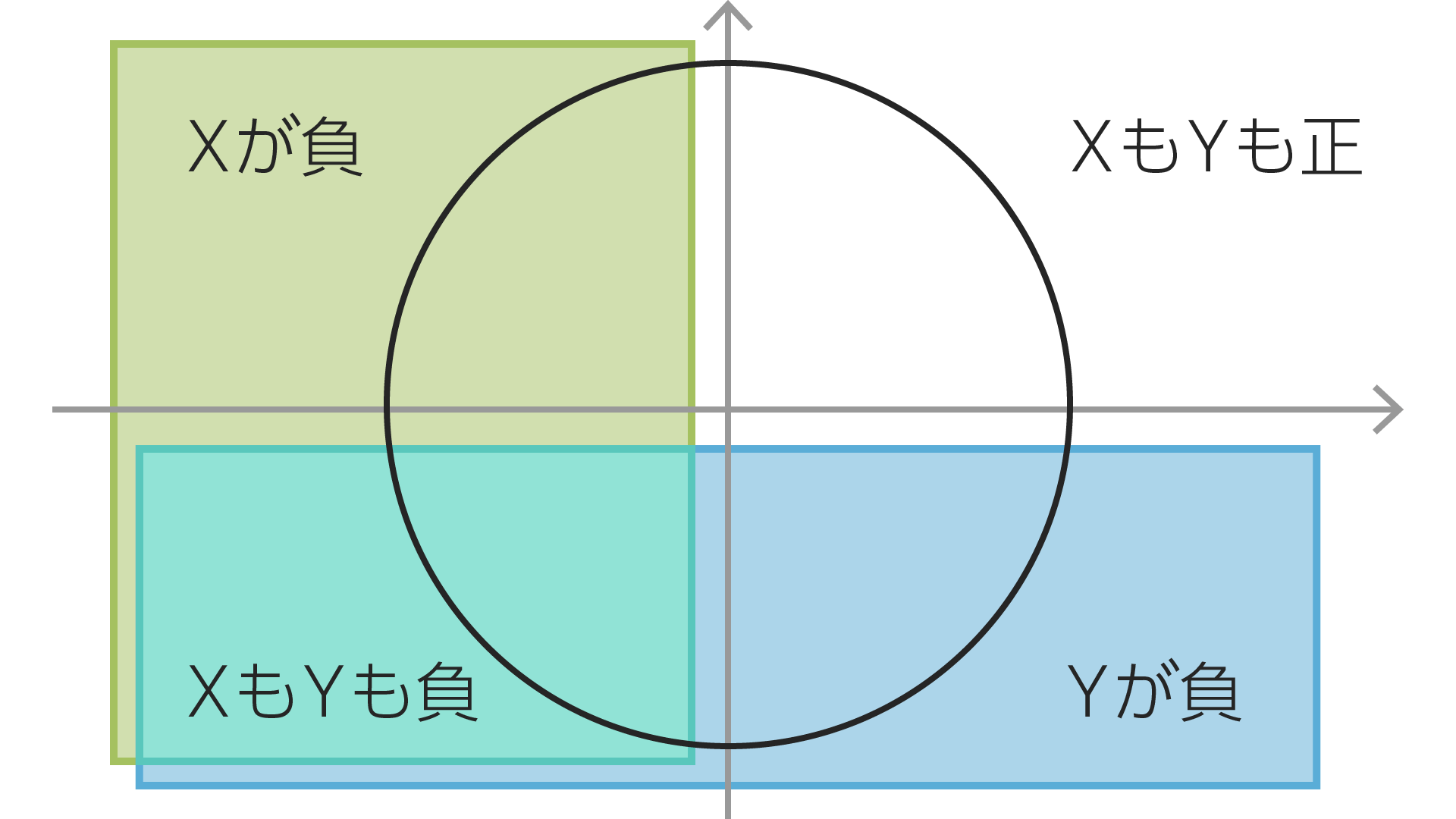
sin,cos,tanの定義から次のことが言えます。
- $\sin\theta$はエリア1・2では正であり、エリア3・4では負になる。
- $\cos\theta$はエリア1・4では正であり、エリア2・3では負になる。
- $\tan\theta$はエリア1・3では正であり、エリア2・4では負になる。
基本問題
$\tan\theta=-\frac{4}{3}$で$\cos\theta=\frac{3}{5}$であった。この時の$\sin\theta$の値を求めよ。
答え（ぼかしをタップするとみれます）
$\sin\theta = -\frac{4}{5}$
解説を詳しく見る 見なかったことにする
$\tan\theta$が負の数ということはθはエリア2かエリア4にある。$\cos\theta$が正の数ということはθはエリア1か4にある。この二つの条件を満たす必要があるので$\theta$はエリア4にある。したがって$\sin\theta$は負になる。
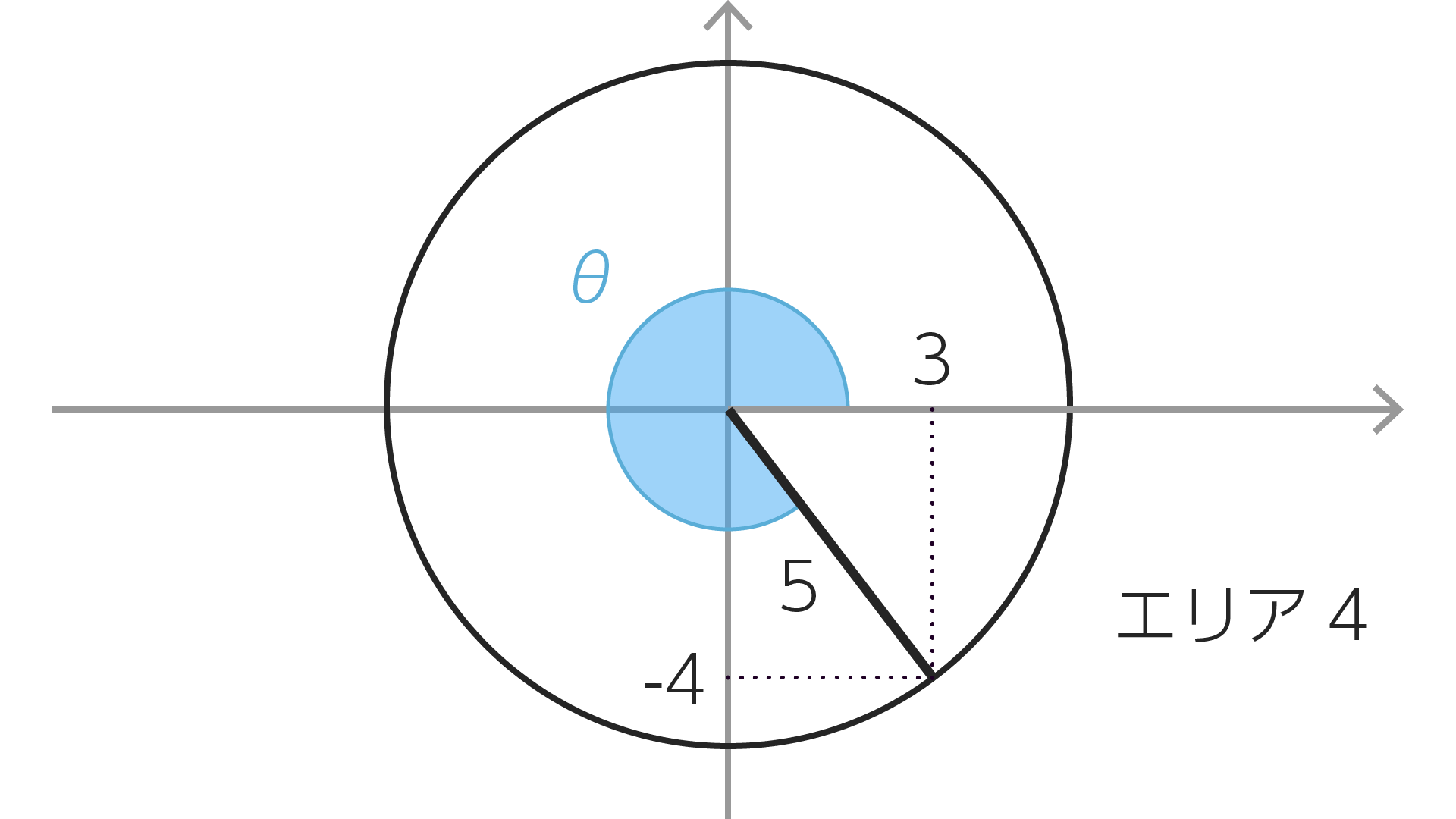$$\begin{split}
\cos\theta&=\frac{X}{r}\\
&=\frac{3}{5}\\
\\
\tan\theta&=\frac{Y}{X}\\
&=\frac{-4}{3}
\end{split}$$
したがって$X=3,Y=-4,r=5$である。
$\sin\theta=\frac{Y}{r}$なので
$$\begin{split}
\sin\theta &= \frac{-4}{5}\\
&=-\frac{4}{5}
\end{split}$$
（以上）
発展問題
$\tan\theta$を$\sin\theta$と$\cos\theta$を使って表せ。
答え（ぼかしをタップするとみれます）
$\tan\theta = \frac{\sin\theta}{\cos\theta}$
解説を詳しく見る 見なかったことにする
$$\begin{split} \sin\theta&=\frac{Y}{r}\\ r\times\sin\theta&=Y\\ \\ \cos\theta&=\frac{X}{r}\\ r\times\sin\theta&=X\\ \\ \end{split}$$ のように$\sin\theta,\cos\theta$を変形する。したがって$X=r\times\cos\theta, Y=r\times\sin\theta$である。 $\tan\theta=\frac{Y}{X}$なのでX,Yにそれぞれ$r\times\cos\theta, r\times\sin\theta$を代入する。 $$ \begin{split} \tan\theta&=\frac{r\times\sin\theta}{r\times\cos\theta}\\ &=\frac{\sin\theta}{\cos\theta} \end{split}$$ （以上）
三角関数の用途
ここから先は理解することを目的としたものではなく「三角関数って身近にあったんだ！」という気づきを大切にする部分なのでサラッと読むだけで大丈夫です。
みなさん今日は電気は使いましたか？照明をつけたり、電子レンジで調理したり、エアコンをつけたり…などなど。それだけでもうあなたは三角関数のお世話になっています。
コンセントにくる電圧はプラスとマイナスが一秒間に60回#6切り替わる交流です。
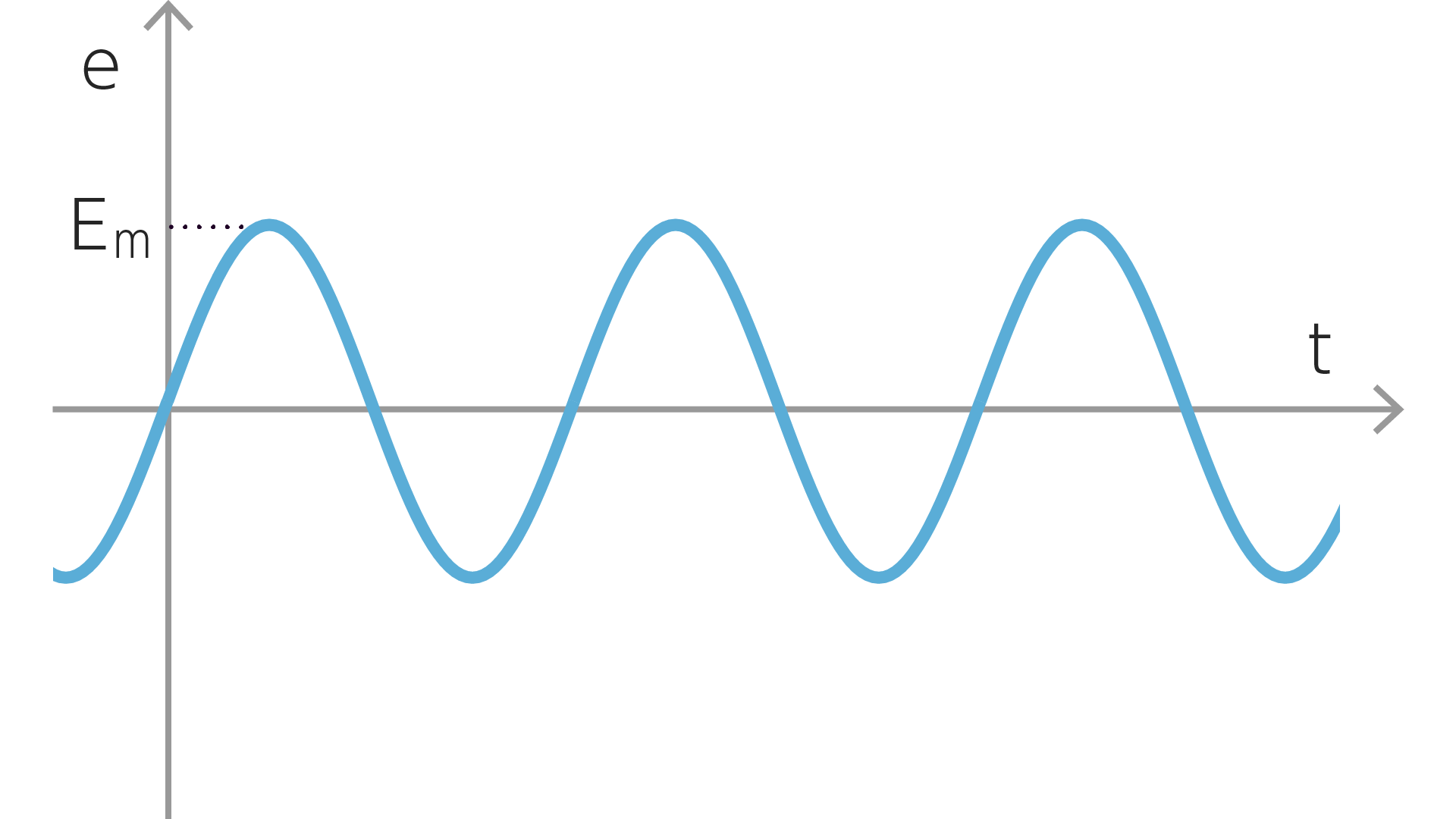
この交流の式はこのような式になっています。
\[e(t)=E_m \sin\omega t\]覚えておいてほしいのはこの式自体ではなく、三角関数がないと僕たちは電気を使うことはできないということ。
電気だけではありません。カーナビの位置表示や地図を作るときに行う測量、ゲームの計算や飛行機や船の航行、音楽など世の中あらゆるものに使われています。今この記事を読むために使っているスマートフォンやパソコンも三角関数に支えられています。
三角関数は身の回りに溢れています。
三角関数は決して一部の理系の人のためのものではありません。
おわりに
かなりの長文でしたが最後まで読んでくださってありがとうございました。初めてsin,cos,tanを見た人はとても難しく感じたかもしれません。しかしここまで読み切れたということに自信を持って良いと思います。
この記事を通して人間社会と三角関数は密接に関わっているということに気づいてもらえたら嬉しいです。
では、これから良い三角関数ライフをお送りください！👋
（万が一計算の間違い等あればDM等で教えていただければ幸いです。）
参考文献
- 新基礎数学 - 大日本図書
#1 あるわけない
#2 高専生のこと
#3 中学3年数学 三平方の定理
#4 小学4年算数 縮図・拡大図
#5 お気づきかと思いますがこれは第一、第二、第三、第四章限に相当します。
#6 世界の中心は岐阜です。東日本は50回（=50Hz）らしい。
おすすめ記事
積分して寝正月脱却した話
少し遅くなりましたが新年明けましておめでとうございます。 僕は典型的な寝正月を過ごしていたわけなんですが、その時...
三角関数RTA
工学と密接に関わりを持つ三角関数ですが、もちろんロボットの制御にも欠かせないものとなっています。母なる三角関数を知...
Comments