三角関数RTA
工学と密接に関わりを持つ三角関数ですが、もちろんロボットの制御にも欠かせないものとなっています。母なる三角関数を知らずに理論的にロボットを制御することはできないと言っても過言ではないでしょう。
私たちが三角関数に頼らねばならない一方で、三角関数の演算は加算や乗算と比べると遥かに時間のかかるものであることも事実です。
そこで今回は色々な方法で三角関数の値を求め、どの方法が高速かを実際に計測してみることにしました。
三角関数RTA開幕です。
⏳RTA:
Real Time Attackの略で開始してから終了までの時間の短さを競うこと。主にゲームなどで用いられる用語。
おしながき
今回RTAに参加する選手の皆さんをご紹介いたします。
- 標準の三角関数
- テーブルをもとに一次関数で近似
- 多項式近似
- マクローリン展開で近似
さて王冠を手にするのは誰だ！？れでぃーふぁいと💪
対象とする関数
このRTAの対象となる関数はこちらです。
\[\sin{x}(0 \leq x < \frac{\pi}{2})\\\arctan{x}(0 \leq x < 78.5)\]$\sin{x}$は三角関数の定番ですね。東京に行って東京ばな奈をお土産に買ってくるくらい定番の関数です。
$\arctan{x}$は$\tan{x}$の逆関数で傾きから角度に変換できるのでこれも結構よく使います。Arduino系だとatan(double x)とかatan2(double x, double y)という関数が用意されています。
実験環境
- Arduino UNO
- $\sin{x}$は0.001刻み、$\arctan{x}$は0.05刻みで計算する。
こんな感じです。今回は鋭角のみですが、鋭角の三角関数の値が分かれば残りも求められるのでこのような条件で行きます。$\sin{x}$と$\arctan{x}$の試行回数を揃えたいのでこのような条件になってます。
今回のコーディングにはPlatformIOのArduino Frameworkを用います。
1. 標準関数を用いる
sin(x), atan(x)を用いて計算してみます。これが最もポピュラーな方式かなと。今回はこの数値をベースに検証を進めます。
実行結果：
sin: 184292
atan: 314420
sin(x)が1.84×10⁻¹[s]、arctan(x)が3.14×10⁻¹[s]でした。この値には変数への代入やfor文でぐるぐるする時間等も含まれているので純粋な三角関数の計算のみを積算した値ではないことに注意してください。
💡ソースコードについて:
最後に最適化サボり防止とありますが、これがないとコンパイラが「計算してもこの変数使わないんだったら計算しなくてよくね？」って言って計算を省くという最適化を行うので追記してあります。普段はこれによって処理速度を向上させることができているのですが、今回は計測という目的にそぐわないのでそれを防ぐためにこうなってます。
2. テーブルで近似
あらかじめそれっぽいテーブルを用意しておいて、それで近似します。配列に入れてそれを読み出すだけだと、配列に入っていない値が入力された時に対処できないので、値が近い2点を通る一次関数として近似します。
$\arctan{x}$は傾きが1を境に反転することでテーブルの容量を減らしました。ちょっとでも速くしたいのでベタ打ち多めです。
今回は単純な速度比較のために省いていますが、配列の要素の範囲を超えてメモリにアクセスしてしまう脆弱性があるため実際に組み込むとなればif文等でガードする必要があります。
実行結果：
sin: 19356
atan: 178424
どちらもまぁまぁ速くなりましたね。$\arctan{x}$の方は割り算があるので処理が重めになっています。しかしこれなしで配列の要素数でゴリ押そうとすると多分ROMを使い切ってしまうので仕方ありません。
3. 多項式近似
Excelで近似曲線を求め、それを三角関数の代替とする戦法です。今回は処理の速さと正確性のバランスから$\sin{x}$には三次関数、$\arctan{x}$には二次関数を選択しました。ソースコードではxを括ったりして乗算の回数を減らしています。
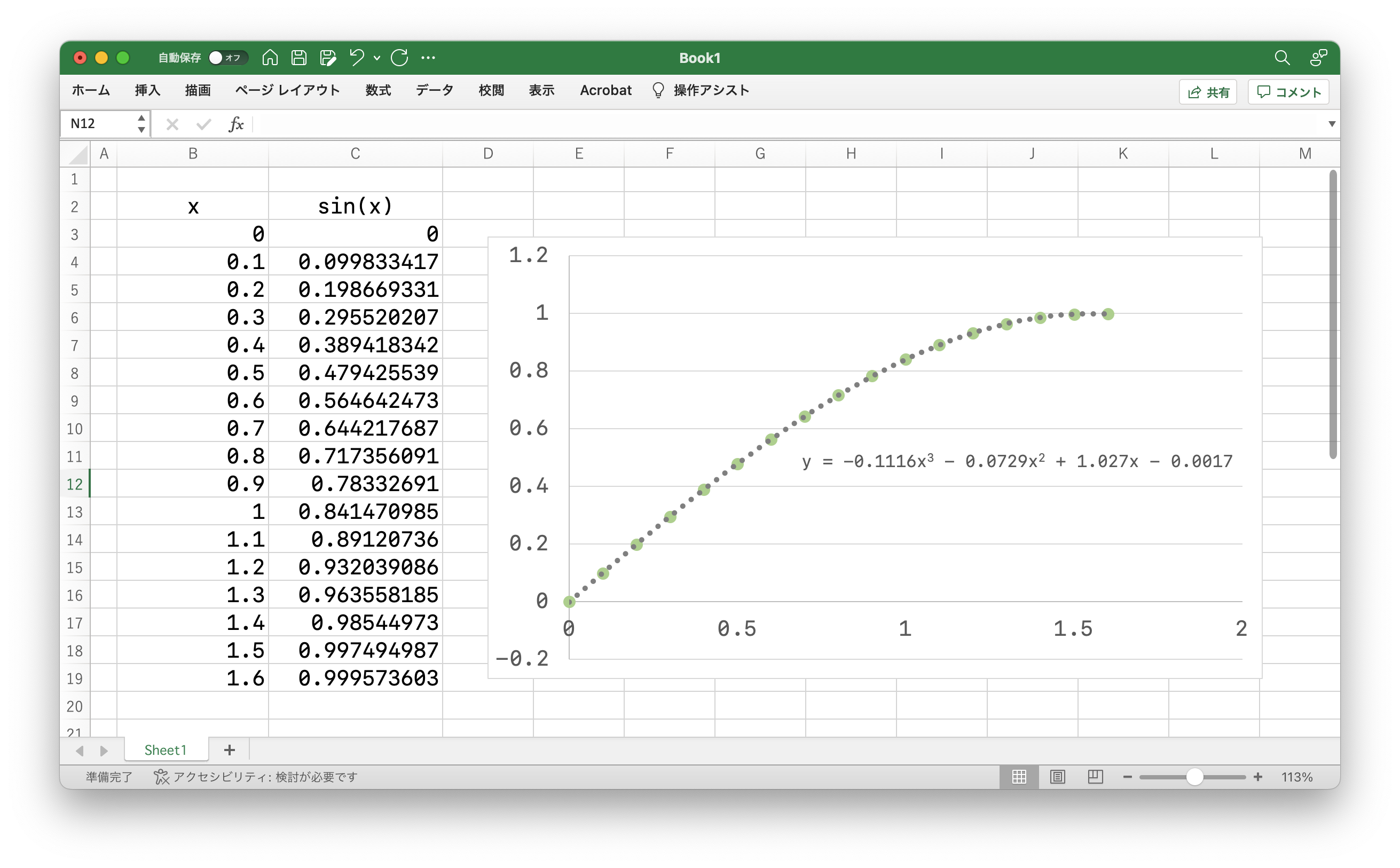
実行結果：
sin: 18128
atan: 135584
はい〜！！かなり高速化できました。ソースコードもシンプルですし、テーブルを用意しなくていいのもいいですね。$\arctan{x}$の方はif文と除算が加わるため少し遅くなっています。三角関数RTA暫定1位です。
4. マクローリン展開
マクローリン展開を用いて近似するという戦法です。マクローリン展開を使うと微分可能な関数を（条件等いろいろありますが）多項式に展開することができます。
\[\begin{aligned} f(x)&=\sum_{k=0}^{\infty} f^{(k)}(0) \frac{x^{k}}{k !}\\ &=f(0)+f^{\prime}(0)x+\frac{f^{\prime \prime}(0)}{2 !} x^{2}+\frac{f^{\prime\prime\prime}(0)}{3 !} x^{3} \cdots \end{aligned}\]なんかむずくてわからんって人は、結論のソースコードだけ見てもらっても大丈夫です。
ではまず$\sin{x}$について考えていきましょう。
\[\begin{aligned} (\sin{0})^{\prime}&=1\\ (\sin{0})^{\prime\prime}&=0\\ (\sin{0})^{\prime\prime\prime}&=-1\\ \cdots \end{aligned}\]なので、
\[\begin{aligned} \sin x &= \sum_{k=0}^{\infty}\frac{(-1)^k}{(2k+1)!}x^{2k+1} \\ &= x - \frac{1}{3!}x^3 + \frac{1}{5!}x^5 - \frac{1}{7!}x^7 + \cdots \end{aligned}\]というシンプルな多項式で表すことができます。確かにちゃんと奇関数になってますね。
現実問題的に無限に足し合わせていくわけにもいきませんので、今回は$x$の変域は$0\leq x\leq \frac{\pi}{2}$なのを踏まえて
\[\begin{aligned} \sum_{k=0}^{2}\frac{(-1)^k}{(2k+1)!}x^{2k+1} &= x - \frac{1}{3!}x^3 + \frac{1}{5!}x^5\\ &\approx x+0.0083x^3(x^2 - 20) \end{aligned}\]の式で近似します。$x^3$を括り出して計算回数を減らしていることと、120で割らずに$0.008\dot3=\frac{1}{120}$をかけて割り算を避けているのがポイントです。変域が$0\leq x\leq \frac{\pi}{2}$を超える時は周期関数であることを利用してごりごりするだけです。
先ほどの多項式近似よりはいい精度が出るのではないでしょうか。ソースコードはこちらです。
実行結果：
sin: 18136
ちゃんと高速化できました！ただしこの方式では$\arctan{x}$を近似式で求めることができません。理由は長くなるので折りたたんで記述しました。
白熊のがんばりを見てあげる 見なかったことにする
一応理解して書いているつもりではいますが、ちょっと怪しいかもなので他の文献と照らし合わせながら参考程度に読んでね
まず$\frac{d}{dx}\arctan{x}$を求めていきます。 $$ y=\arctan{x}\Leftrightarrow x=\tan{y} $$ $$ \begin{aligned} \frac{dy}{dx}x&=\frac{d}{dy}\tan{y}\frac{dy}{dx}\\ 1&=(\frac{1}{\cos^2{y}})\frac{dy}{dx}\\ \frac{dy}{dx}&=\cos^2{y}\\ &=\frac{1}{1+\tan^2{y}}\\ &=\frac{1}{1+x^2} \end{aligned} $$ これは初項1、公比$-x^2$の無限等比級数なので、 $$\begin{aligned} \frac{1}{1+x^2}&=\sum_{k=0}^{\infty}(-x^2)^k\\ &=\sum_{k=0}^{\infty}(-1)^kx^{2k}\\ &=1-x^2+x^4-x^6\cdots \end{aligned} $$ あとはこれを積分すれば$\arctan{x}$のマクローリン展開を導出できます。 $$\begin{aligned} \arctan{x}&=x-\frac{1}{3}x^3+\frac{1}{5}x^5-\frac{1}{7}x^7\cdots\\ &=\sum_{k=0}^{\infty}\frac{(-1)^k}{2k+1}x^{2k+1}\\ \end{aligned}$$ となります。 しかし、これが成り立つには$|x|< 1$である必要があり、つまり$\frac{\pi}{4}$以上の角度は返ってきません。$\sum_{k=0}^{\infty}(-x^2)^k$が$|x| \ge 1$で発散することを考えれば容易に想像できると思います。
さらにさらに$|x| < 1$の範囲でさえ精度よく求めるには途方もない回数計算しなくてはならず、むしろ標準関数より遅いので、今回は$\arctan{x}$をこの方法で求めるのは無理という結論になりました。
こんなに長いTeX書くの初めてだからどっか間違ってるかも…。見つけたらやさしく教えてください。
まとめ
多項式近似とマクローリン展開が無双するという結果になりました。テーブルを用いた手法も悪くはなかったですが、ROMを占有すること踏まえるとコスパが悪いかもしれません。
しかし、「処理が遅い遅い」と嘆いている皆さん、それ本当に三角関数のせいで遅くなっているのでしょうか？近似に除算を必要とする$\arctan{x}$と必要としない$\sin{x}$の処理時間にはかなり開きがありますが、除算の有無を除けば行なっている処理自体はそこまで変わっていません。
除算が時間のかかる処理であることをご存知の方は少なくないと思いますが、他にも実際にロボットを動かそうとなると他マイコンとの通信やデータの読み取りなどで時間のかかる処理は山ほどあります。通信や除算などの重い処理に目を瞑り、「処理が重いのは三角関数のせい」と一意に片付けてしまうのは非常にもったいないことです。
三角関数の高速化に取り組む前に、もう一度ご自身のソースコードを舐め回すように眺めてみてください。もし、それでも処理が遅いと感じているなら、この記事をもう一度覗きにきていただければ幸いです。
おすすめ記事
積分して寝正月脱却した話
少し遅くなりましたが新年明けましておめでとうございます。 僕は典型的な寝正月を過ごしていたわけなんですが、その時...
オムニホイール制御指南
RCJをやっている人なら一度は聞いたことがあるオムニホイールという部品。 これとモーターのセットを3セット以上使...
Comments