ベクトル入門

唐突ですがベクトルというものをご存知でしょうか。英語ではvectorと言います。
高校生の方はもしかしたら数学の授業でやっているかもしれません。高専生の僕は夢の中にベクトルが出てくるくらいやらされている教えていただいているのですが、今日はそのベクトルについてのお話を珈琲でも嗜みながら書いていこうかなと。
概要 - Abstract
この記事では主にベクトルの概念と基礎計算を軽く扱います。またロボットにおけるベクトルの使い道の例を軽く紹介します。
この記事では解説にあたって「〇〇が理解できない場合、××の知識が足りないかも」というように、解説を理解するために必要な予備知識についても明示しました。もし読んでいる最中に理解につまづいたらそれも併せて確認してみてください。
小中学生のお友達がこの記事を読む場合、文字とかが多くて少しむずかしい!って感じるかもしれません。でもノートに書き出してみたり、算数・数学の先生や理科の先生に聞いてみたりすることで時間はかかるかもしれませんが理解できるようになるはずです。
対象読者
- ロボット製作にあたって線形代数を学んでみたい方
- 数学で背伸びしたい小中学生
- 学生に戻りたい大人の皆さん
高校生、高専・大学生の方には簡単すぎて物足りないかもしれません。
Note
本編に入る前にこの記事で説明しないこと、省いて説明することをあらかじめ明示しておきます。厳密な表現を求める方以外はこの項は飛ばしてもらって構いません。
- 複素数・複素ベクトルについては触れません。
- 2次元ベクトルのみを扱います。3次元以上のベクトルについてはこの記事では解説しません。
- 内積・外積には触れません。
正直なところ厳密な表現を求めるほどガチな人はこの記事読まないとは思いますが…。
ベクトルとは?
3, 12, π, $\frac{3}{5}$ などは一般的にスカラーと呼ばれます。中学生までの数学は基本的にこれを扱います。
スカラーは大きさの情報のみを持ちます。例えば、1は3よりも小さいです。πは$\frac{7}{5}$よりも大きいです。
これに対して大きさと向きの二つの情報をもつものをベクトルと言います。

例えば、重さや長さや時間などは共通の単位(kg, m, s)などをあらかじめ決めておくことで一つの実数で表すことができます。「体重が52kgだ」とか「家から学校まで500mある」などなど。いわばただの数値です。つまりこれらはスカラーです。
対して速度や力などは大きさだけではなく向きも表す必要があります。「敵艦隊が西に時速40kmで移動中」や「社長が部下へ圧力をかけた」なども向きが明確になっていますね。これがベクトルです。
例えば「岐阜駅から2km離れたところにいるから電車ついたらきてね。」と言われても「いや、北か南か東か西かどっちやねん!」ってなりますね。ちゃんと「岐阜駅から北に2km離れた店にいるね。」などと言ってもらえない限り辿り着くことは難しいでしょう。
普段意識することはありませんが、このように私たちの生活にはベクトルの概念が欠かせないものとなっています。
ベクトルの表記
では実際にベクトルを扱っていきましょう。
例としてベクトルOAを定義してみます。これは点Oを始点、点Aを終点とするベクトルを意味します。
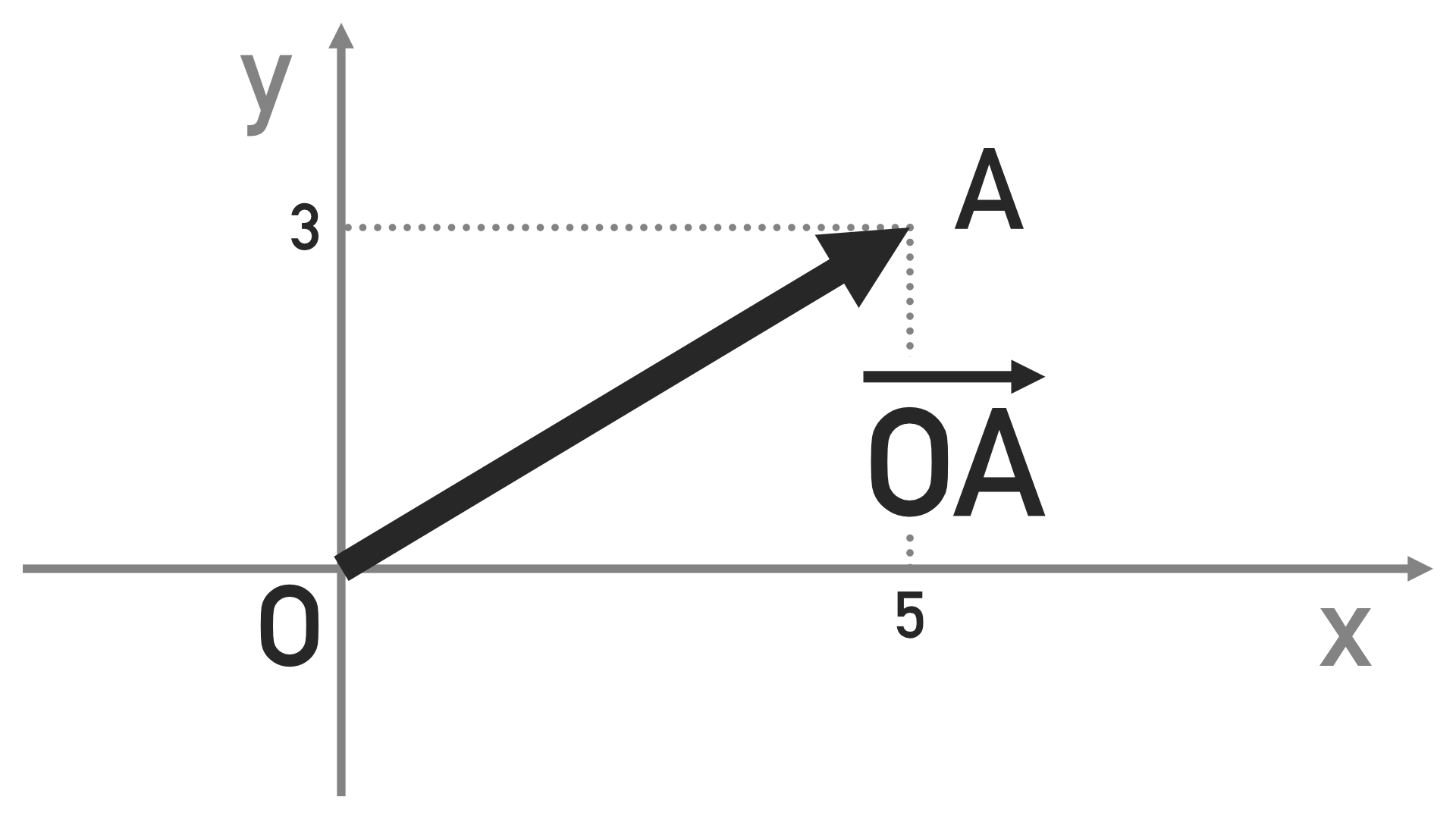
このベクトルの長さのことをベクトルの大きさ、向いている方向のことをベクトルの向きといいます。
💡 この解説がうまく理解できない場合
座標の概念の理解が足りていない可能性があります。方眼ノートに実際に手でこのベクトルの図を書いてみることをお勧めします。
ベクトルOAを文字で表す時には$\vec{OA}$のように文字の上に矢印をつけて表記します。
教科書や流派によっては矢印をつけずに太字にするだけだったりしますが、この記事では上に矢印を書く表記を採用します。大切なのは表記の仕方そのものではなく、それがベクトルかスカラーかのどちらかを常に意識することです。
では実際に数式を扱っていきましょう。$\vec{OA}$のx軸方向の距離は5、y軸方向の距離は3なので、
\[\vec{OA}=\binom{5}{3}\]と表します。この時、5と3のことを$\vec{OA}$の成分と言います。
Note: 教科書や参考書によっては
$ \vec{OA}=(5,3) $ という横向きの表記になっているかもしれませんが、意味は全く変わりません。 個人的には見やすさと行列の表記との整合性を踏まえると縦向きの方が分かりやすいと思います。
ベクトルの和
では実際にベクトルを用いて計算をしてみましょう。
\[\vec{\alpha}=\binom{x_{\alpha}}{y_{\alpha}},\vec{\beta}=\binom{x_{\beta}}{y_{\beta}}\]とするときこの二つのベクトルの和は次のように定義されます。
\[\begin{split}\vec{\alpha}+\vec{\beta}&=\binom{x_{\alpha}}{y_{\alpha}}+\binom{x_{\beta}}{y_{\beta}}\\&=\binom{x_{\alpha}+x_{\beta}}{y_{\alpha}+y_{\beta}}\end{split}\]文字や添字が多くなってきたことでこんがらがってきている人がいるかもしれません。まず一旦深呼吸してみましょう、そこまで難しくないはずです。
\[\binom{◯}{□}+\binom{△}{☆}=\binom{◯+△}{□+☆}\]こうすればどうですか?上の段同士、下の段同士を足す。これがベクトルの和の定義です。
💡 この解説がうまく理解できない場合
文字と式の関係について理解できていない可能性があります。小学校6年生の算数「文字を使った式」について学習することをお勧めします。
ではこれを図示してみます。

平行四辺形の対角線になっていることに気づきましたか?
このようにベクトルを使うとすごくシンプルに図形の計算ができるようになることを実感できたと思います。
練習問題
\[\vec{A}=\binom{5}{3},\vec{B}=\binom{4}{2},\vec{C}=\binom{1}{7}\]の時、次を求めよ。
$1.\quad\vec{A}+\vec{B}$
$2.\quad\vec{A}+\vec{C}$
$3.\quad\vec{B}+\vec{C}$
答え(ぼかしをタップするとみれます)
$1.\quad\binom{9}{5}$
$2.\quad\binom{6}{10}$
$3.\quad\binom{5}{9}$
💡 この問題がうまく解けない場合
和の計算方法やベクトルの概念が理解できていない可能性があります。少し戻ってもう一度読み直してみましょう。
もし時間と余力があるなら余った方眼紙に今やったベクトルの計算を図示して平行四辺形の対角線になっているかを確認してみましょう。これでベクトルの和はバッチリですね👌
逆ベクトル
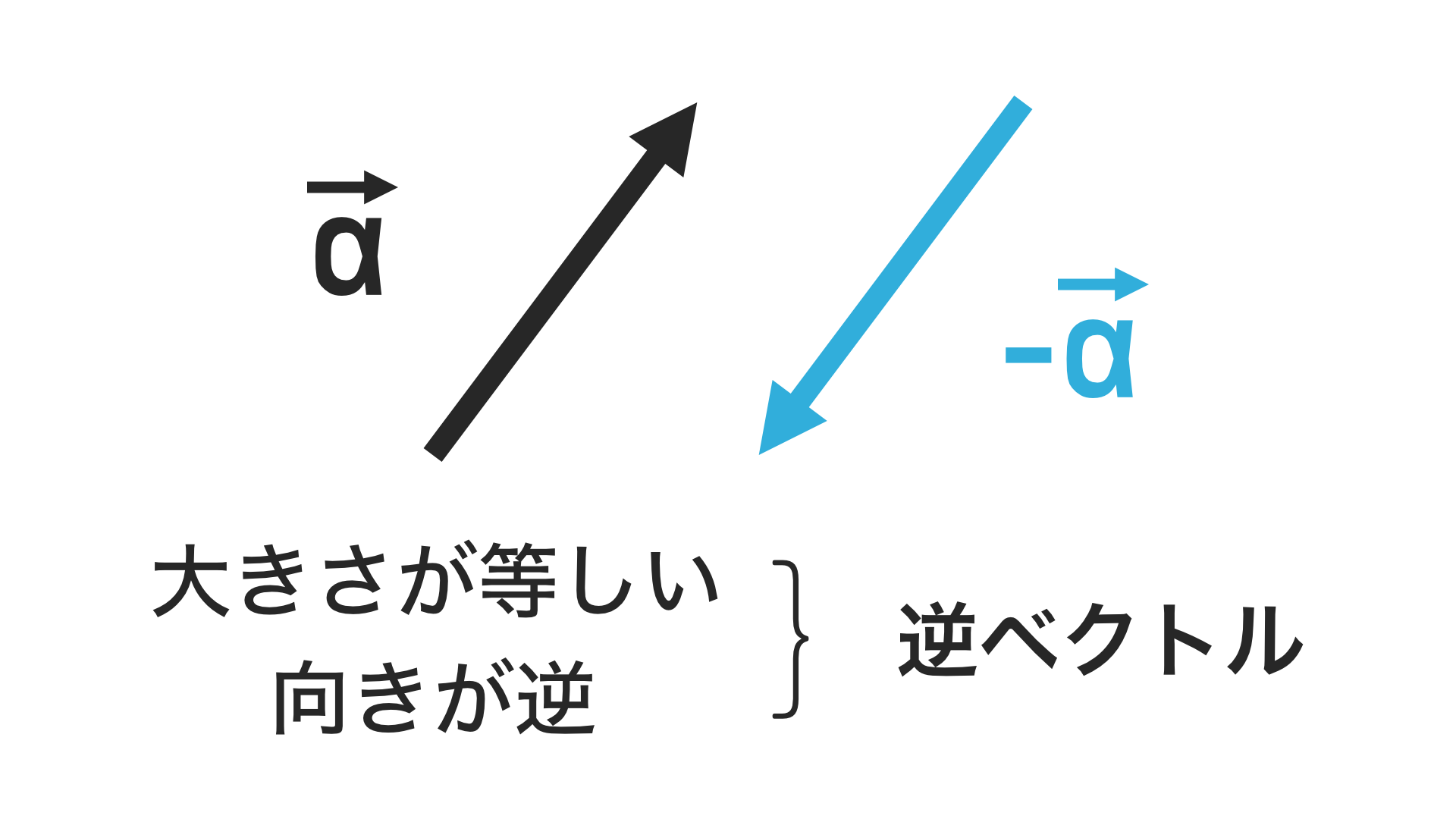
図を見れば一目瞭然だと思います、矢印の長さは同じだけど向きが正反対。記号は単純に-をつけるだけです。
少し頭を捻って考えてみると、ベクトルの引き算は逆ベクトルを足すことと言えます。
\[\vec{A}-\vec{B}=\vec{A}+(-\vec{B})\]💡 この解説がうまく理解できない場合
負の数(マイナスがつく数)の足し算、引き算、掛け算、割り算を理解できていない可能性があります。中学校1年生の数学の単元「正負の数」を学習することをお勧めします。
スカラー倍
スカラー倍のイメージはこちらです。向きは変わらず長さが変化します。ただし掛ける数が負の数の場合は向きが逆になることに注意してください。
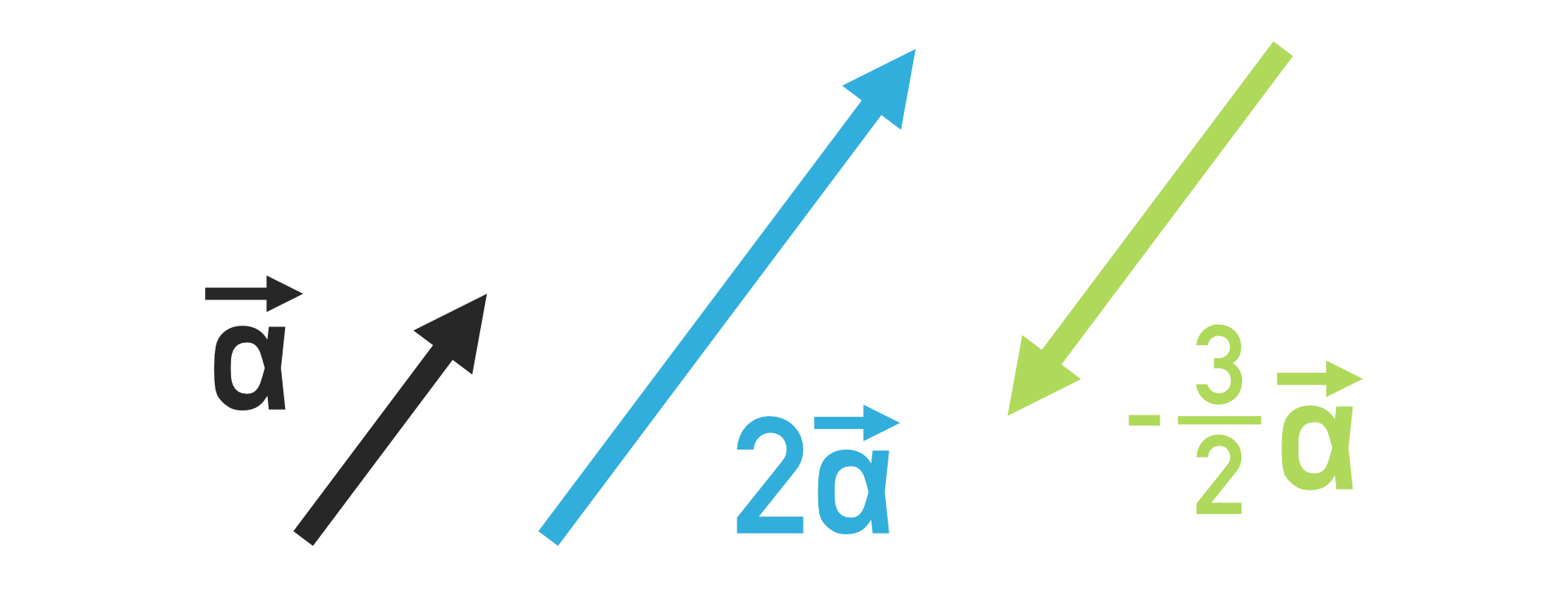
実際にやっている計算は上の式のようにベクトルのそれぞれの成分に掛け算するだけです。
注目ポイントは、文字$k$には矢印がついていませんね。つまり$k$はベクトルではなく実数です。つまりこのスカラー倍とはベクトル同士の掛け算ではありません。
編集 2022/05/01
$k\in\mathbb{R}$に関する記述が初心者にはちょっと分かりにくそうだったので表現を改めました。また誤解を防ぐため「掛け算」の単語を「スカラー倍」に改めました
総復習問題
#1
\[\vec{A}=\binom{6}{1},\vec{B}=\binom{-5}{3},\vec{C}=\binom{2}{4}\]とするとき、次を求めよ。
\[\begin{split}&1.\quad2\vec{A}-3\vec{B}\\&2.\quad\vec{A}+\vec{C}-2\vec{B}\\&3.\quad4(\vec{B}+2\vec{C})\end{split}\]答え(ぼかしをタップするとみれます)
$1.\quad\binom{27}{-7}$
$2.\quad\binom{18}{-1}$
$3.\quad\binom{-4}{44}$
💡この問題がうまく解けない場合
ベクトルの足し算とスカラーとの掛け算がうまく理解できていない可能性があります。また「ベクトルの引き算」が「逆ベクトルを足すことと同じである」ということを理解できていない可能性があります。少し戻ってもう一度読み直してみましょう。
#2
次のとき、$x,y$に入る数を求めよ。
\[\binom{5}{y}+2\binom{x}{\frac{1}{2}x}=\binom{9}{6}\]答え(ぼかしをタップするとみれます)
$x=2,y=4$
#2の解き方
\[\begin{split}\binom{5}{y}+\binom{2x}{x}=\binom{9}{6}\end{split}\]従って、
\[\begin{cases}5+2x&=9\\y+x&=6\end{cases}\\x=2,y=4\]💡この問題がうまく解けない場合
ベクトルの足し算とスカラーとの掛け算がうまく理解できていない可能性があります。また中学校2年の数学「連立方程式」を理解できていない可能性があります。
ロボットの制御でベクトルが役立つ部分
例えばオムニホイールを用いたロボットを制御したいとします。ロボカップジュニアでも上級者が使うことも多いですね。
オムニホイールとは?
車輪の外周に小さな空回りする車輪を多く備えた特殊な車輪です。モーターの回転方向に対しては普通の車輪のように振る舞いますが、回転方向と垂直の向きには滑るという性質を持っいます。


このホイールを3つ以上のモーターと組み合わせて使うことでロボットが向いている方角を変えずに全方向に移動することが可能になります。
やってみよう
今回はこのように90度づつに4つ配置したモデルで考えてみます。
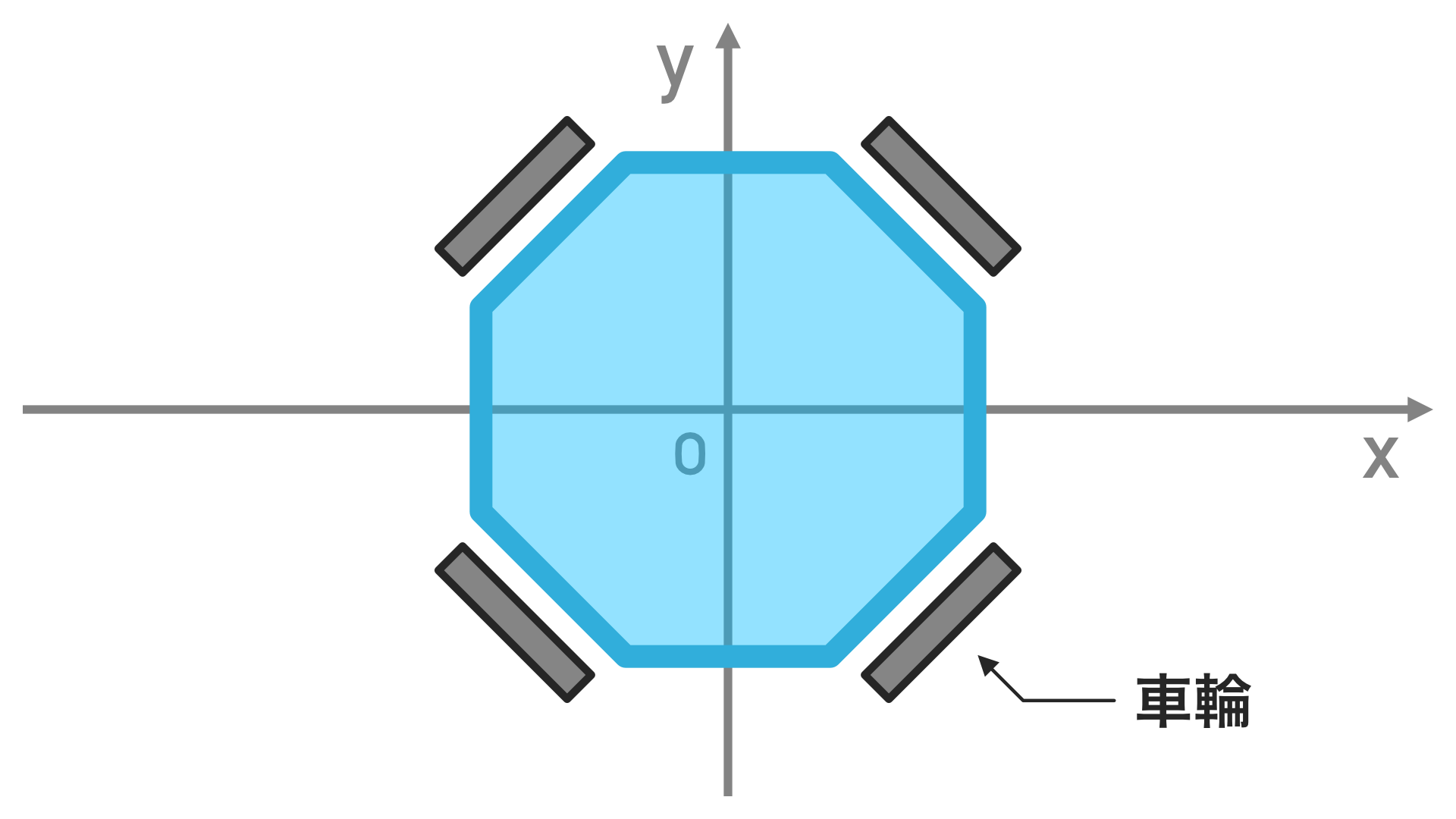
では下の図のようにモーターを矢印のように回転させたらどのように動くでしょうか。
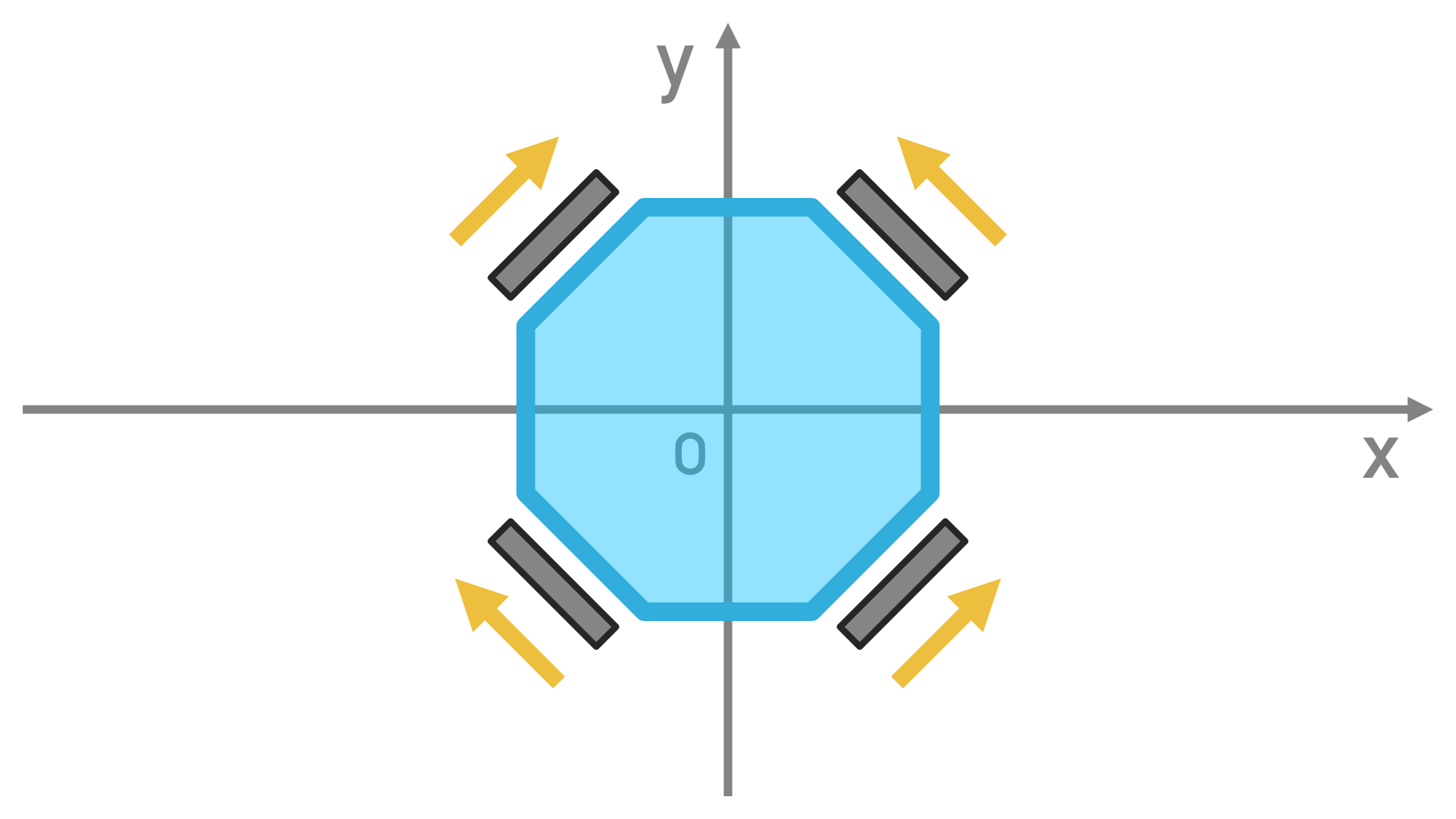
直感的には前に進むというのがなんとなくわかると思います。これを直感ではなく数学的にベクトルを使って説明してみましょう。
モーターの回転によって生まれる橙色の矢印で示した力のベクトルを足し合わせてみましょう。すると足し合わせたベクトルは前向きを向いています。つまりロボットは前進します。
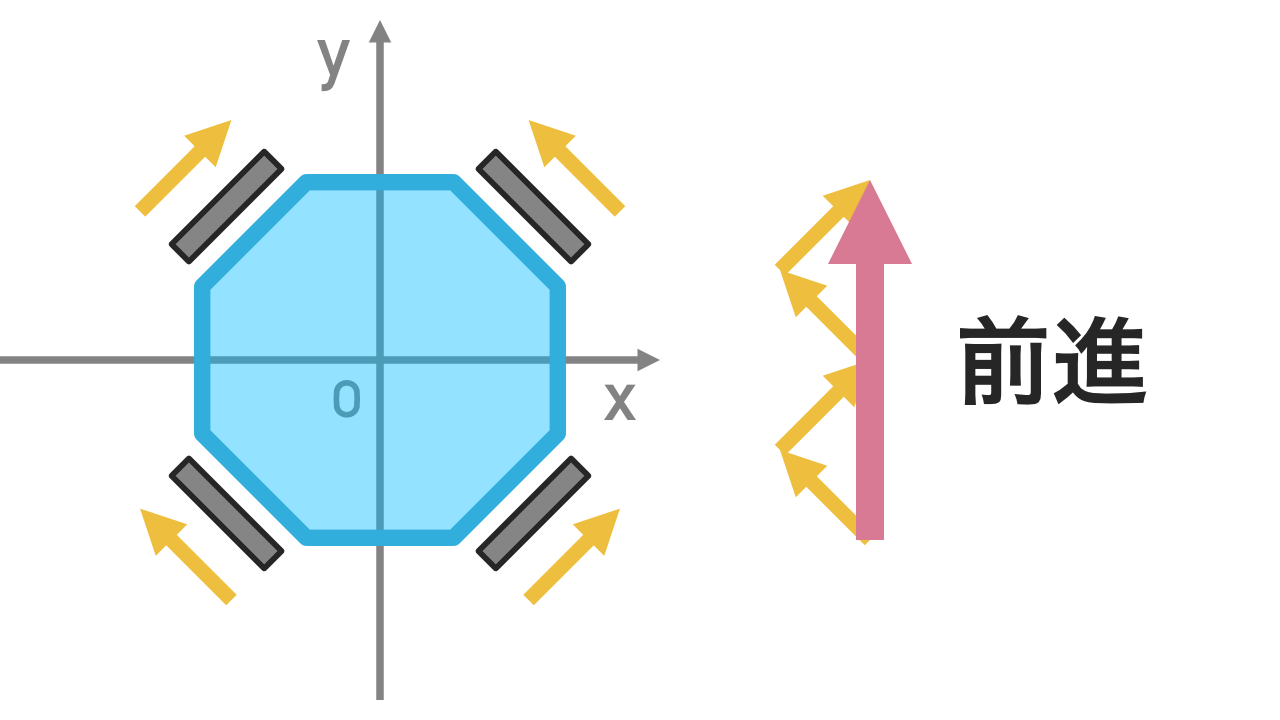
このような考え方をしていくことで45度刻みでなくても、360度どの方向でも好きな方向に進むように制御ができるようになります。右に進みながらちょっと後ろに進むといったような絶妙な制御もお手のものです。
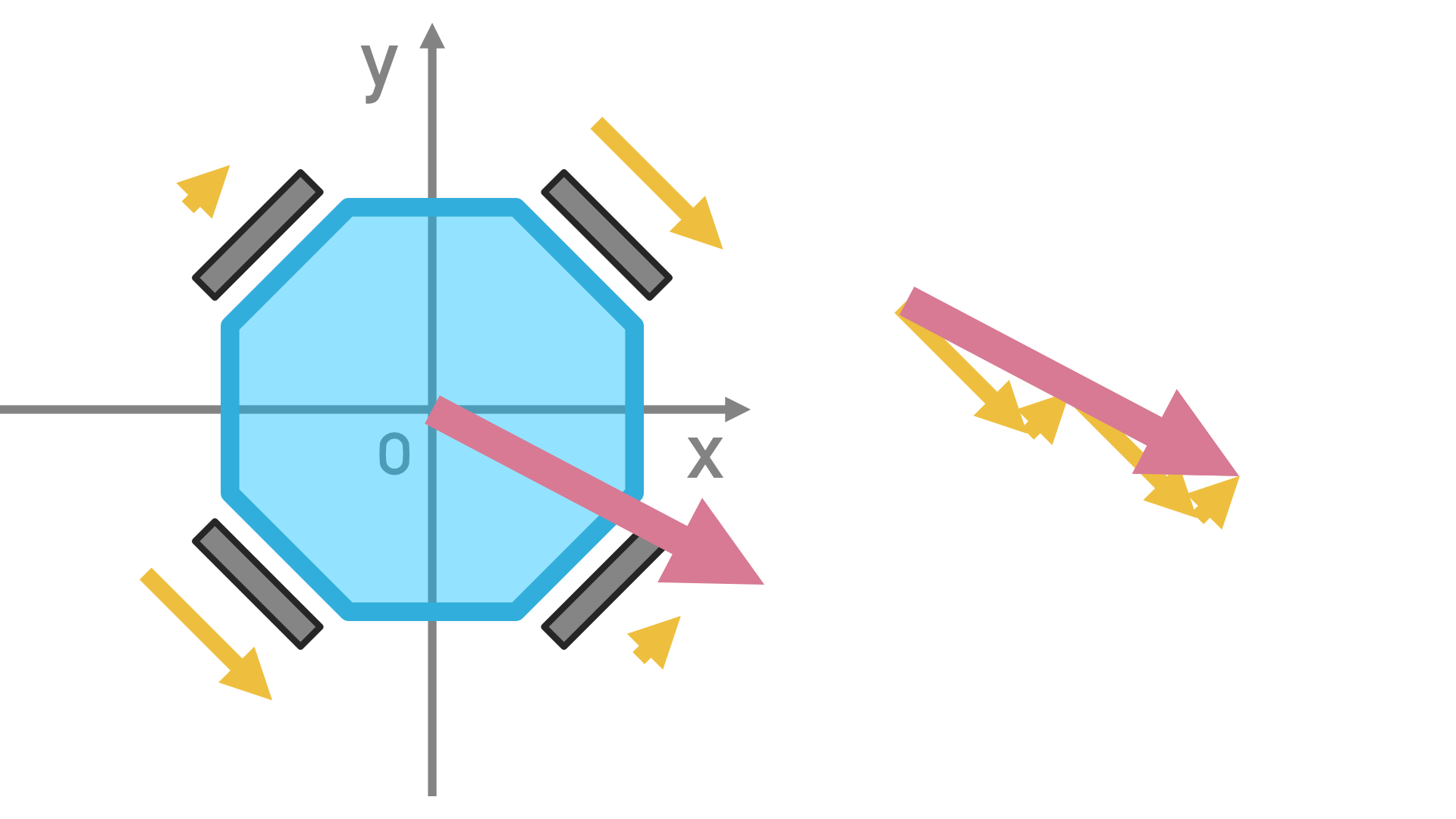
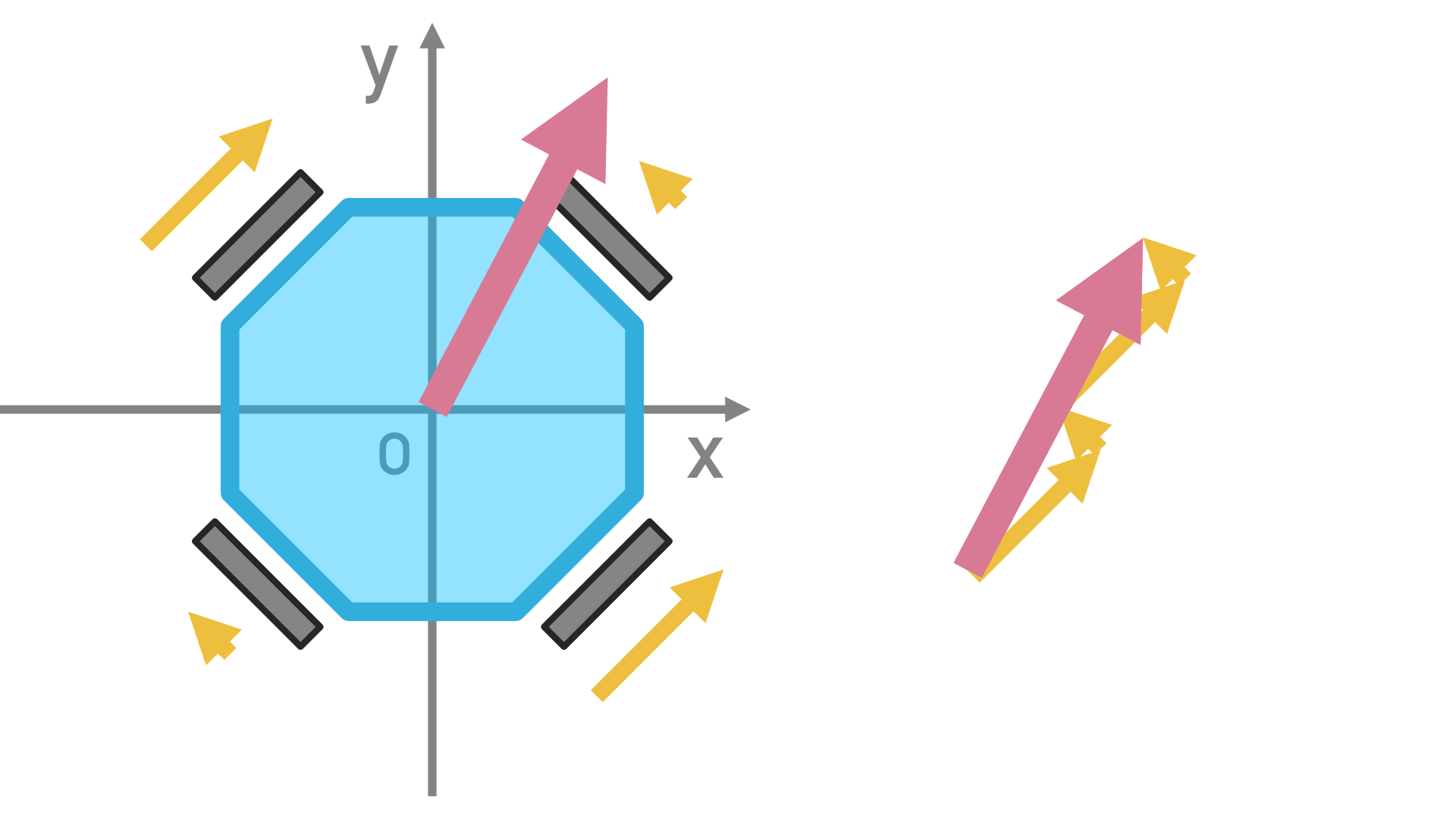
終わりに
この記事ではベクトルの性質や使用方法まで詳細には扱いませんでしたが、この記事を通して今まで使ったことのなかったベクトルについての概念やイメージを掴んでいただけたら幸いです。
オムニホイールの移動についても実際に計算しようとなると三角比の知識が必要になってきますが、それよりもまずは脳内でベクトルのイメージを持つことが大切です。このイメージさえ持っていれば三角比について学んだ時にスムーズにオムニホイール制御を理解できると思います。
僕自身も線形代数の”せ”も理解できていない程度ですが、この記事がこれから線形代数を学び始める人のとっかかりにでもなってくれたら嬉しいです。
ではまた✌️
(計算の間違い等あればDM等で教えてほしいです。修正します。)
参考文献
- 新線形代数 - 大日本図書
- 機械学習のエッセンス - 加藤公一



Comments