積分して寝正月脱却した話
少し遅くなりましたが新年明けましておめでとうございます。
僕は典型的な寝正月を過ごしていたわけなんですが、その時にともくん（@fTomo_robotと雑談しましてね、
🐻❄️「最近一年早くない？」
🐰「ねー、小学校の頃とか長かったのに。」
🐻❄️「俺らもうおじさんだわ（）」
みたいな話をしたんですよ。確かに一年の体感時間が短くなってる気はするので、電話しながら今人生の何パーセントくらいが終わったのかを計算してみたっていうちょっとした小話です。
Note:
まばたきすら勿体無く感じるレベルのしょうもない記事です。何か面白いものを期待している方はいますぐブラウザバックしませう。
ジャネの法則
年月の長さが年齢によって異なるということを心理学的に説明したジャネさんという方がいるらしいです。
簡単に言えば、生涯のある時期における時間の心理的長さは年齢に反比例すると主張したものである。
例えば、50歳の人間にとって1年の長さは人生の50分の1ほどであるが、5歳の人間にとっては5分の1に相当する。よって、（中略）50歳の人間の10日が5歳の人間の1日に当たることになる。（Wikipediaより）
具体的に立式すると、生まれて最初の一年間の体感時間を1とした時の年齢xにおける体感時間yは次式で表せるそうです。
\[y=\frac{1}{x + 1}\space\space(x \geq 0)\]そもそもこの式が本当に体感を反映しているのかどうかについては気にしないことにします
たのしい積分
今まで生きてきた期間について考えてみます。0歳の記憶がある人はまぁほぼいないと思うので、意識が芽生えた瞬間を記憶元年（以下$t_0$）とし、現在の年齢を$t$とします。
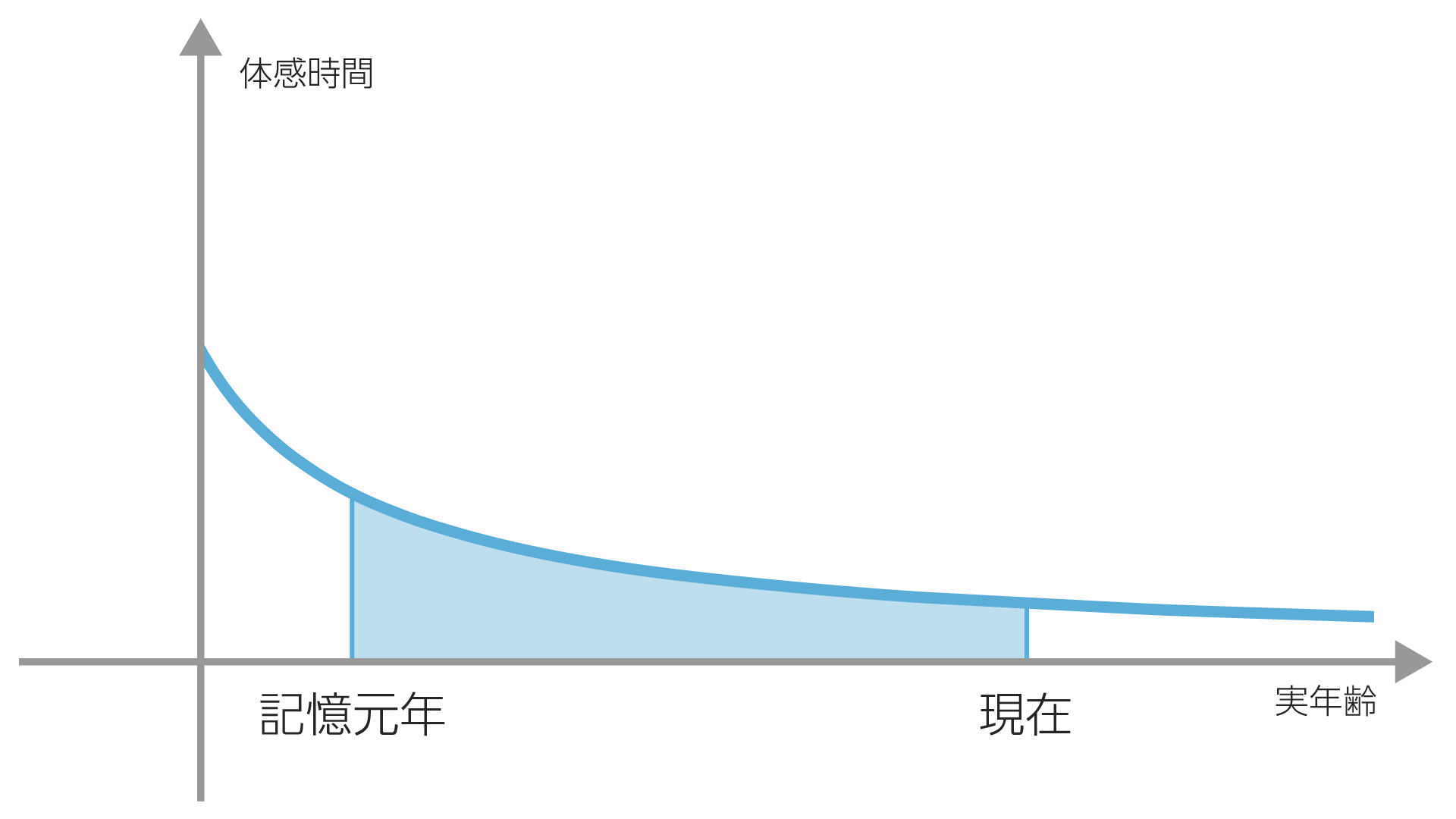
他のネットのサイトにも似たような解説が載っていますが、個人的に意思決定をしてこなかった乳児期に人生の大部分を食われるのが悔しかったので負け惜しみということで。0歳の頃の記憶がある方や、産声からが人生という方は以下の$t_0$を0に読み替えてください。
この色の塗った部分の面積を今までの人生とします。こちらは定積分すれば求められるので
\[\begin{split} \int_{t_0}^{t}\frac{1}{x+1}dx&=\Bigl[\space\log _e |x+1|\space\Bigr]_{t_0}^t\\ &=\log _e |t + 1| - \log _e |t_0 + 1|\\ &=\log _e \left|\frac{t+1}{t_0 + 1}\right| \end{split}\]っと。まぁ人参の皮剥きくらいの難易度じゃないでしょうか。負の数になることはないので絶対値はいらないですが数学の先生に怒られたくないのでつけました。
というわけで人生の今までの体感時間$f(t,t_0)$を以下のように定義します。
\[f(t,t_0)=\log _e \left|\frac{t+1}{t_0 + 1}\right|\]人生の進捗いかが？
僕は今年の8月に18歳になって、覚えている一番昔の記憶は幼稚園年少なので$t=18,t_0=4$の時の$f(t,t_0)$は約1.335です。
星になる年齢$t_{max}$を80歳として$f(t_{max},t_0)$を計算してみると約2.772なので…
約48%も終わっています！！！！
あとがき
人生の約半分がすでに終わってるという悲しい現実が発覚しました。気付くのが遅かった気もしますが、これから人生後半頑張ります。
怖くなってこの計算した次の日は大阪日本橋の共立電子まで足を伸ばしてM5Stackを買ってきました。このまま寝ててはまずいと。これからは襟を正して生活したいと思います。（※思います。）
みなさんも人生のこりどれくらいか計算してみてくださいね。背筋が凍りますよ。
おわり
おすすめ記事
MFT2023
10/15に東京国際展示場で行われたMaker Faire Tokyo 2023に行ってきました。前日まで全然行く...
Swiftで遊んでみた
最近自分が興味を持っている言語でSwiftというものがあります。 AppleがiOS、Mac、Apple TV、...
Comments