オムニホイール制御指南

RCJをやっている人なら一度は聞いたことがあるオムニホイールという部品。
これとモーターのセットを3セット以上使うことで、前を向いたまま姿勢を崩さずに全方位に移動するというチートみたいな動きができるようになります。実際に近年の全国大会に出場するサッカーのチームのほとんどはオムニホイールを採用しています。
オムニホイールを使用した実際の動きの例です。このデモではジャイロ・地磁気センサ等の姿勢を取得できるセンサを用いていませんが、かなり精度良く前を向いて動けています。研究・微調整の賜物です。
概要 - Abstract
この記事は主に制御式を理解して導出することを目標にした記事です。行列を知らない方も多いのと思うのでベクトルの和のみで話を進めます。
対象読者
- オムニホイール制御に初めて挑戦する方
- 式の意味を理解してオムニホイールを制御したい方
この記事を読み進めるにはベクトル入門と三角関数入門の内容を既に理解できている必要があります。
理解せずに最後の章だけ見て自分のロボットのプログラムに制御式を組み込むのも悪くはないですが…。せっかくなので、ね?
オムニホイールのベクトル合成の仕組みについてはベクトル入門の最終章で紹介しているのでそちらを参照してください。
導入
今回は4輪のモデルを使って説明していきます。動径は時計回りを正とし、正面を北とし0°とします。東が90°で南が180°で西が270°です。
今回は並行移動(=回転せずにまっすぐ前を向いたまま移動する)を前提条件とします。回転したい人はモーターをいい感じにぐるぐるしてください。
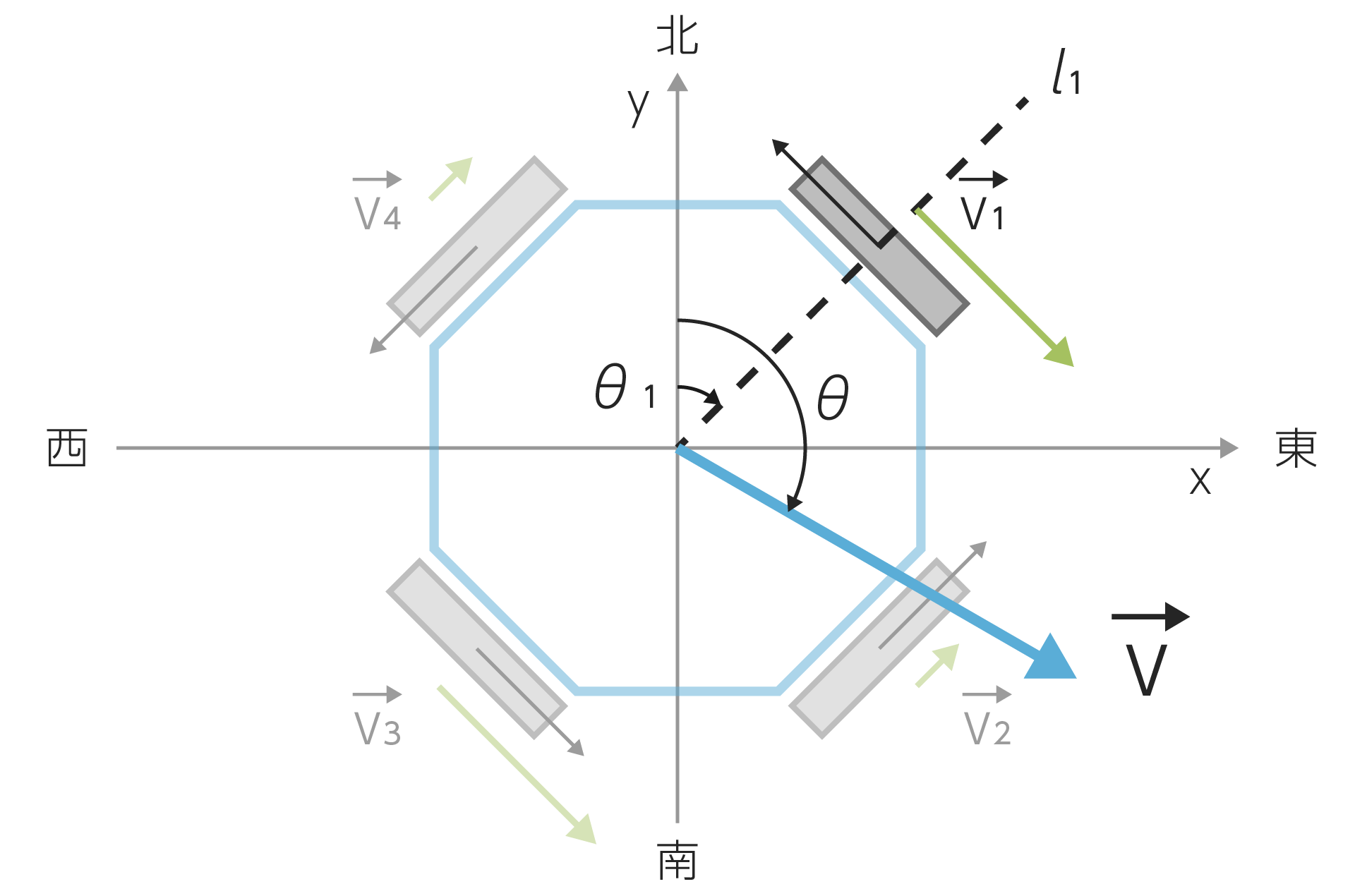
| $\vec{v_n}$ | 各モーターの速度ベクトル(緑) |
| $\theta_n$ | 各モーターの取り付け角(図では$\theta_2$以降は省略) |
| $l_n$ | 各モーターの取り付け角を図示した線 |
| $\theta$ | ロボットの進行方向 |
| $\vec{v}$ | ロボットの速度ベクトル(青) |
記号多いですが頑張りましょう。ここをちゃんと押さえることで制御の仕組みが後の説明を読んだときに腑に落ちやすくなります💪
記号の矢印を取ると大きさという意味になることも同時に押さえておきましょう。
- $v$は$\vec{v}$の大きさ(=$\vec{v}$の矢印の長さ)→ ロボットの速さを表す
- $v_n$は$\vec{v_n}$の大きさ(=$\vec{v_n}$の矢印の長さ)→ 各モーターの速さを表す
モーターが正転する方向は車輪から生えている黒い矢印の向きで示しています。つまりこのモデルの場合、全てのモーターを正転させると反時計回りに回ります。
また、モーターの取り付け角$\theta_n$はお使いのロボットに合わせて変更してください。例えば上の図のモデルだと$\theta_1=45^\circ,\theta_2=135^\circ,\theta_3=225^\circ,\theta_4=315^\circ$です。
💡Note
数学的にはx軸方向を0°とし反時計回りを正とするのですが、オムニホイール制御で姿勢制御する際にジャイロセンサーや地磁気センサを搭載することが殆どですので今回はそれに則ります。
ここから先を読み進める際の注意点です
- ベクトルは向きと大きささえ変えなければどこに動かしても構わない
- モーターやロボットの図は全て省略されている(ベクトルしか書きません)
- 右上のモーターのみに注目して話を進めます(他の三つは全て省略します)
この三点を踏まえて上の図を簡略化するとこうなります。($\vec{v_1}$は今から求めるので記入していません。)
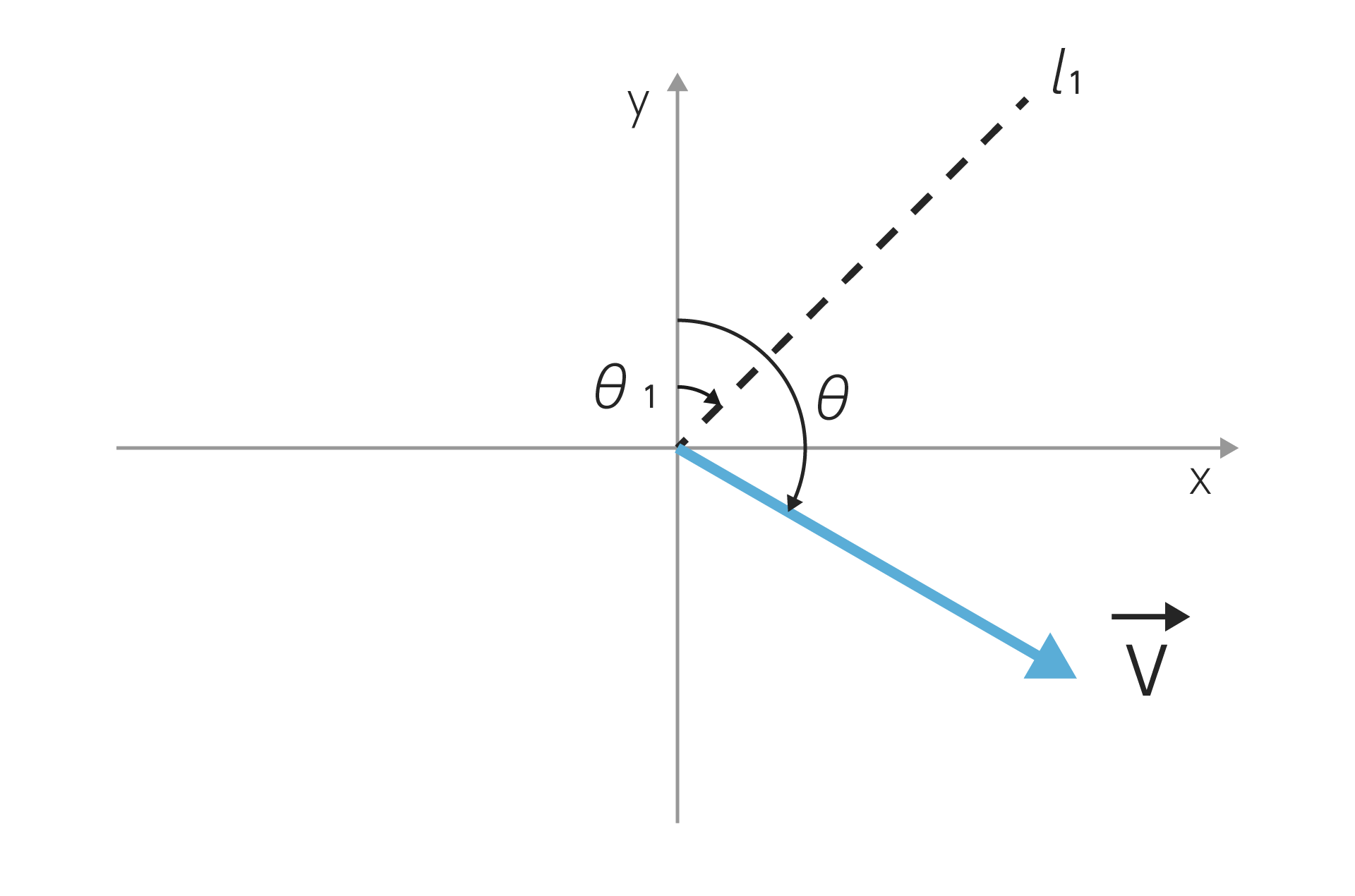
すごくシンプルになりましたね。ではこの図を使って実際に導出していきましょう。
回転させて考える
先ほどの図ではモーターの取り付け角が斜めになっていて式を立てる際にわかりにくいので、全部まるっと$\theta_1$だけ反時計回り(=負の方向に)回転させて$l_1$が$y$軸に重なるようにしてみます。
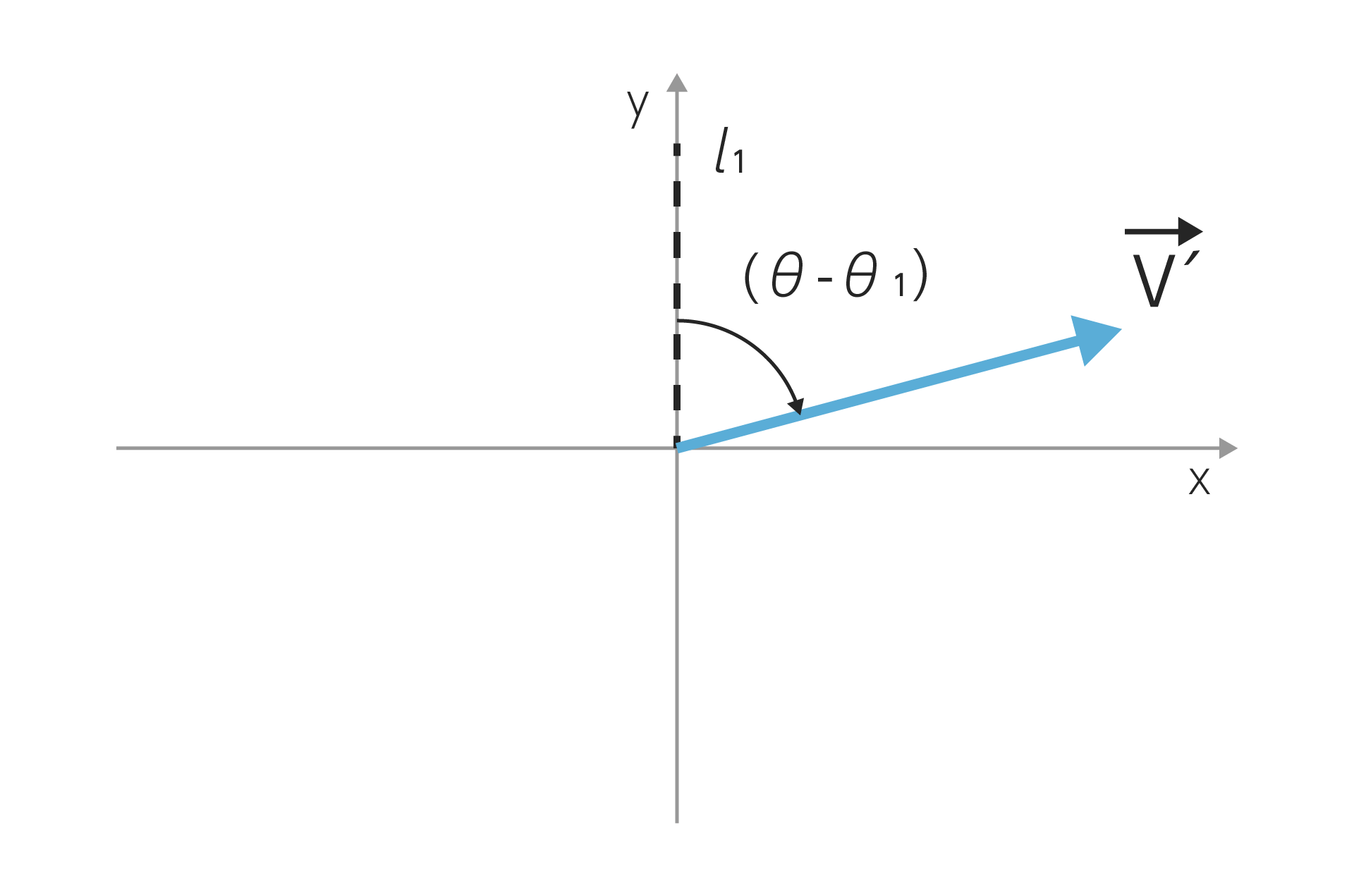
元々$\theta$の方向を向いていた$\vec{v}$を負の方向に$\theta_1$だけ回転させた$\vec{v’}$は$(\theta-\theta_1)$の方向を向いています。最初の図と比べると非常にシンプルになりましたね。
ベクトルの分解
ここまできたらあと少しです。$\vec{v’}$を$l_1$に水平な方向の$\vec{v’_y}$と$l_1$に垂直な方向の$\vec{v’_x}$に分解します。
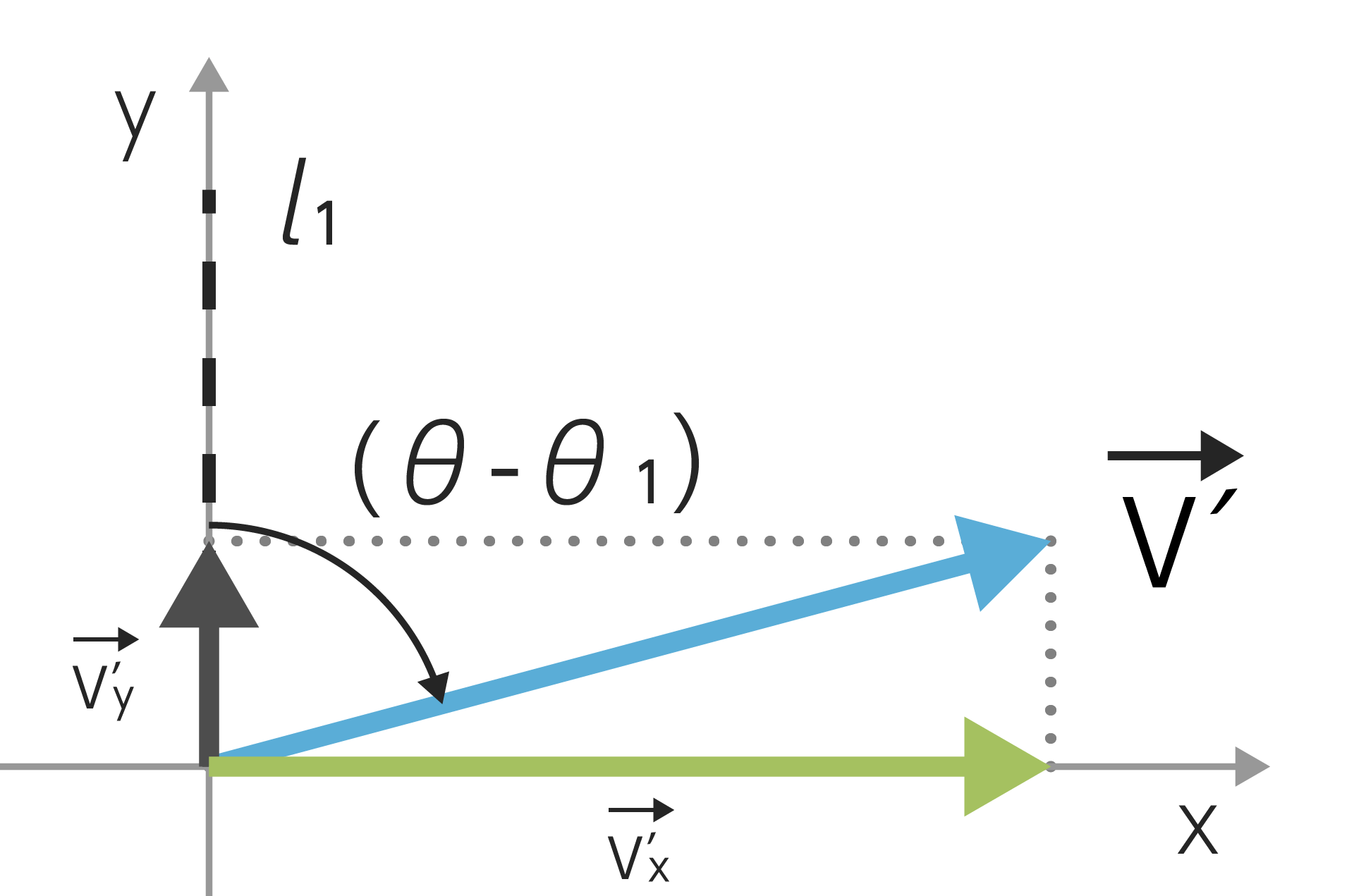
この時三角関数を使うとこのように$v’_x,v’_y$を表せます。
\[\begin{split} v'_x&=v\times\sin(\theta-\theta_1)\\ v'_y&=v\times\cos(\theta-\theta_1)\\ \end{split}\]🤔ここがよくわからない人へ
三角関数入門をもう一回読んでみよう。
$l_1$とオムニホイールの関係を考えてみましょう。下の図は一番最初の図の右上部分を拡大した図です。
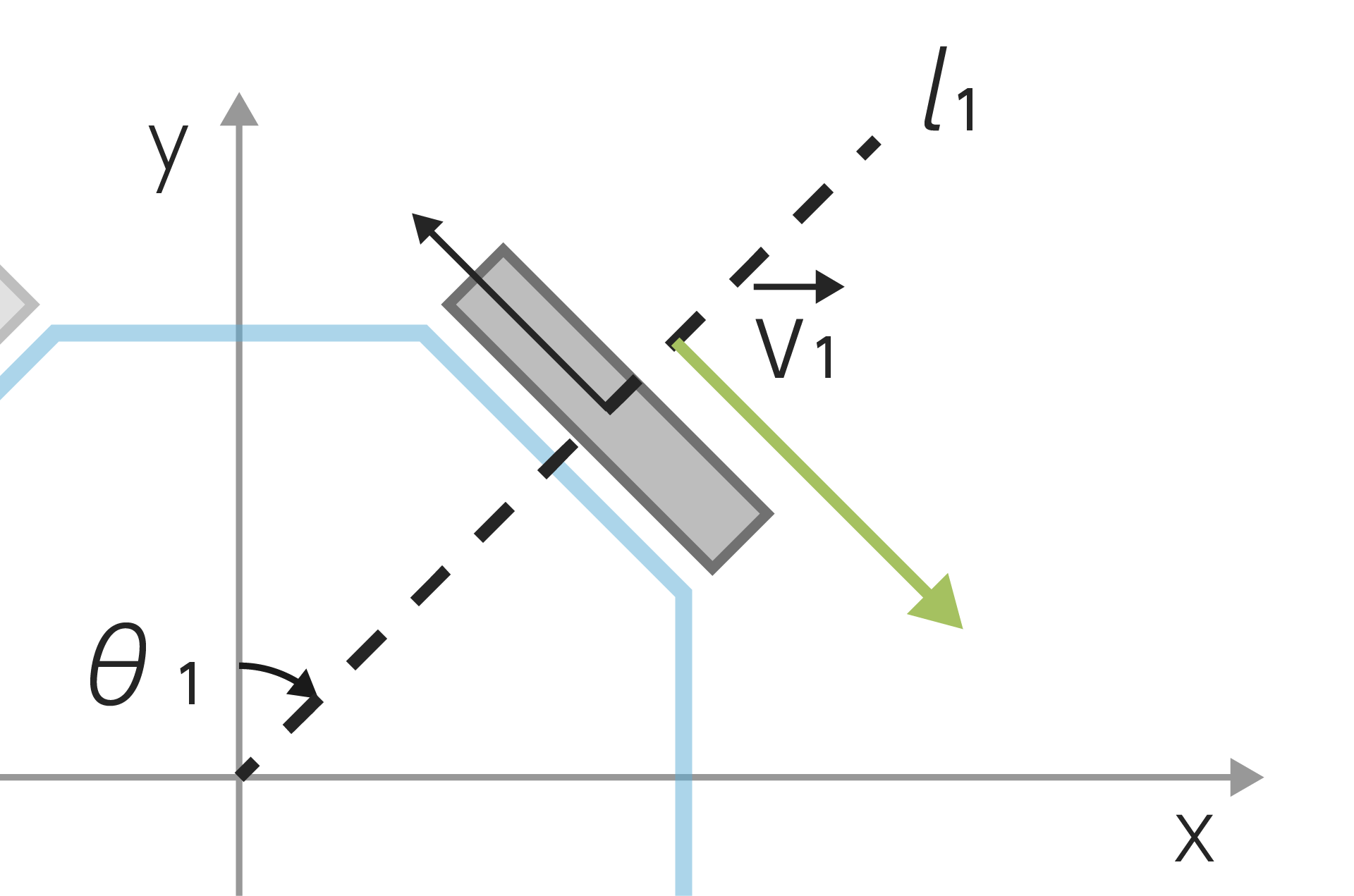
$l_1$はモーターの回転の軸なので、それと並行な$\vec{v’_y}$はサイドホイールの滑りを表します。サイドホイールは動かすものではなく滑るものなのでこちら側から制御することはありません。
対して$l_1$に垂直な$\vec{v’_x}$はオムニホイールの回転を表します。つまりこれがオムニホイールの速度$\vec{v_1}$を表します。
導出結果
以上の計算は$\theta_n$を変えるだけでどのモーターにも適用できます。一般化すると
\[v_n=v\times\sin(\theta-\theta_n)\]になります。この記事を読んでいる方のほとんどが割合(何%とか)でモーターの回転速度を制御すると思いますので、vには0%-100%を入れればOKです。
ガチ勢向け:割合ではなくちゃんと回転数で制御したい人
各モータの角速度$\omega_n$はオムニホイールの半径$r$と$v_n$を使って以下のように表せます。(単位系は統一してくださいね!!!)
$\omega_n=\frac{v_n}{r}$
4輪のロボットの具体的な式 見なかったことにする
X字で90°等間隔配置の場合 $$v_1=v\times\sin(\theta-45^\circ)$$ $$v_2=v\times\sin(\theta-135^\circ)$$ $$v_3=v\times\sin(\theta-225^\circ)$$ $$v_4=v\times\sin(\theta-315^\circ)$$3輪のロボットの具体的な式 見なかったことにする
前開きで120°等間隔配置の場合 $$v_1=v\times\sin(\theta-60^\circ)$$ $$v_2=v\times\sin(\theta-180^\circ)$$ $$v_3=v\times\sin(\theta-300^\circ)$$コード例
Arduinoで実際に使える関数の例がこちらです。
radiansというのは私たちが日常で使う角度の表し方の60分法から、数学の世界で使う弧度法という角度の表し方に自動変換してくれるツールです。Arduino勢でない方も「60分法 弧度法 変換」などで検索するとすぐ引っかかると思います。
終わりに
いかがでしたでしょうか。簡単な説明ではありますがオムニホイール制御式を「理解して使う」ことを目的とした記事を書きました。
オムニホイール制御はぱっと見難しそうに見えますが、ベクトルと三角関数の概念が頭に入っていればすんなりと理解できるものだと思います。
もしわかりづらい表現などあればTwitterか、ブログメニューのContactページから教えていただければ対応します。
次はあなたがプログラムを書いてロボットを動かす番です。大会などで元気よくロボットが動く様子が見られることを楽しみにしています。



Comments